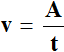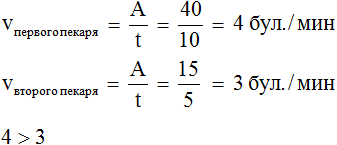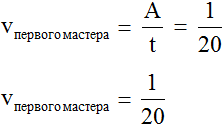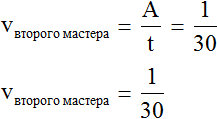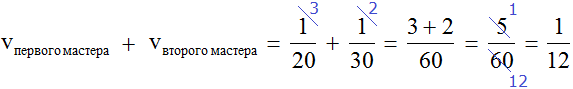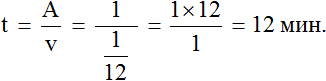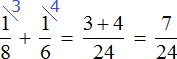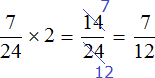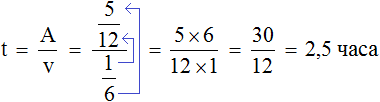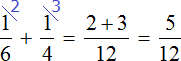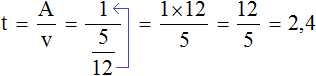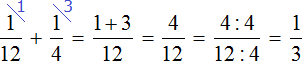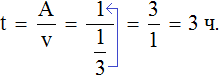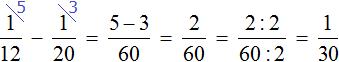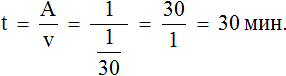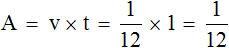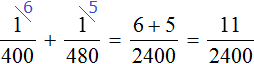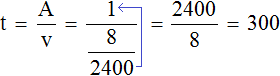Чтобы найти производительность надо работу разделить на время - Контакты компаний и предприятий на Adresa.top

Продолжаем изучать элементарные задачи по математике. Сегодня мы рассмотрим очень интересную физическую величину — производительность.

Что такое сила?

Сила — это физическое явление, способное изменять форму материальных тел, вызывать их движение, менять направление и скорость движения этих тел или приводить тело в состояние покоя.

Примеры сил:

ребята слепили снеговика, а хулиганы его разрушили. Получается, что хулиганы приложили к снеговику свою силу, тем самым вызвали изменение формы снеговика;

на дворе стояла тележка. Прохожий случайно задел её и тележка сдвинулась с места. Получается, что прохожий применил силу к тележке и вызвал её движение;

далее тот же прохожий остановил тележку, чтобы она далеко не уехала. Получается, что прохожий применил силу, тем самым привел тележку в состояние покоя.

Сила является физической величиной — мерой воздействия на тело других тел. Сила обозначается заглавной латинской буквой F.

Что такое работа?

Работа — это количественная мера действия силы на тело. Работа зависит от количества силы, приложенной на тело и от направления этой силы, а также от перемещения данного тела.

Например, если мы попробуем сдвинуть шкаф с места и он сдвинется, то можно сказать, что мы совершили работу, поскольку сила, которую мы приложили, привела к тому, что шкаф совершил перемещение на некоторое расстояние.

Если же мы, к примеру, попробуем толкнуть стену, то стена с места не сдвинется, а значит и работа не будет совершена, поскольку сила была приложена, но эта сила не вызвала никакого перемещения стены.

Работа обозначается заглавной латинской буквой A.

Производительность

Производительностью называют работу, выполненную за единицу времени. Под единицей подразумевается 1 час, 1 минута или 1 секунда. Производительность обозначается латинской буквой v

Рассмотрим следующий пример. Два пекаря пекли булочки. Первый пекарь испёк 40 булочек за 10 минут, а второй 15 булочек за 5 минут. Как узнать, кто из пекарей работал быстрее, первый или второй?

Работал быстрее тот, кто за одну минуту выпекает больше булочек. Говорят, что у него производительность больше. Для нахождения производительности предусмотрено следующее правило:

Чтобы найти производительность, надо выполненную работу разделить на время работы.

Также, можно воспользоваться формулой:

где v — производительность, A — выполненная работа, t — время работы.

Вернемся к нашей задаче. Зная правило или формулу нахождения производительности, можно определить сколько булочек приходится на одну минуту.

Найдём производительность первого пекаря. Разделим работу, которую он выполнил, на время которое он на нее затратил. Выполненная работа это количество испеченных им булочек, то есть 40, а время — 10 минут

40 : 10 = 4 булочки в минуту

Аналогично найдём производительность второго пекаря. Разделим 15 на 5

15 : 5 = 3 булочки в минуту

4 > 3

Первый пекарь в минуту выпекает больше булочек чем второй, значит его производительность выше. Отсюда делаем вывод, что работает он быстрее второго пекаря.

Также можно воспользоваться формулой нахождения производительности. В этом случае решение принимает следующий вид:

Под буквой v можно делать метки, указывающие для кого/чего мы находим производительность.

Задача 2. Тому нужно за 2 дня прочитать книгу, в которой 100 страниц. В первый день он читал 4 часа со скоростью 12 страниц в час. С какой скоростью ему надо читать оставшуюся часть книги, если у него есть на это 4 часа?

Узнаем сколько страниц Том прочитал в первый день. Он читал 12 страниц в час. Чтению в первый день он посвятил 4 часа, поэтому для нахождения количества прочитанных страниц в первый день, нужно 12 умножить на 4

12 × 4 = 48 страниц прочитано в первый день

Узнаем сколько страниц осталось прочесть. Вычтем из общего количества страниц (100) количество прочитанных страниц (48)

100 − 48 = 52 страницы осталось прочесть

Осталось прочесть 52 страницы. Теперь найдем такую производительность, при которой Том сможет прочесть 52 страницы за 4 часа. Раскидаем 52 страницы на 4 часа поровну

52 : 4 = 13 страниц в час

Ответ: чтобы прочитать оставшуюся часть книги за 4 часа, Том должен читать ее со скоростью 13 страниц в час.

Замечание. В некоторых источниках слово «производительность» может быть заменено на слова «скорость», «эффективность», «продуктивность», «плодотворность».

Задача 3. Один насос работал 4 часа, выкачивая 158 вёдер воды в час, а другой — 3 часа, выкачивая 169 вёдер воды в час. Определить какой из насосов выкачал больше вёдер.

Решение

Определим сколько всего вёдер выкачал каждый насос по отдельности. Для этого умножим их производительность на время их работы:

158 в/ч × 4 = 632 вёдер выкачал первый насос

169 в/ч × 3 = 507 вёдер выкачал второй насос

632 > 507

Ответ: первый насос выкачала больше вёдер, чем второй.

Задача 4. За 2 часа насос выкачал 80 литров воды. Определить сколько литров он выкачает за 5 часов.

Решение

Сначала нужно определить сколько литров воды насос выкачивает за час. Для этого 80 литров разделим на 2 часа — получим 40 литров

80 : 2 = 40 литров в час

За один час насос выкачивает 40 литров воды. За 5 часов выкачает в пять раз больше

40 × 5 = 200 литров

Ответ: за 5 часов насос выкачает 200 литров воды.

Если известны производительность и время работы, то можно найти выполненную работу. Выполненная работа равна производительности умноженной на время работы:

A = v × t

Например, если производительность пекаря составляет 50 булочек в час, и он проработал 4 часа, то можно найти всю выполненную работу за эти четыре часа. Для этого производительность (50 бул/ч) нужно умножить на время его работы (4ч)

50 × 4 = 200 булочек

Если известны работа и производительность, то можно найти время работы. Время работы равно отношению выполненной работы к производительности:

Например, если в неделю бригада отстраивает 2 этажа, то можно узнать сколько недель потребуется для отстройки 8 этажей. Чтобы определить время отстройки восьми этажей, нужно выполненную работу (8 этажей) разделить на производительность (2 эт./нед):

8 : 2 = 4 нед.

Либо с помощью формулы, приведенной выше:

Если в неделю строится 2 этажа, то 8 этажей будет отстроено за четыре недели. В данном случае вся работа была равна восьми. Производительность была равна двум, поскольку по определению производительность есть работа, выполненная за единицу времени – в нашем случае два этажа за неделю.

Задача 6. Принтер работает с производительностью 70 стр./ч. Сколько страниц он напечатает за 5 часов?

Решение

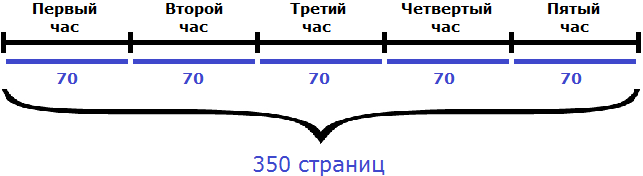
Если в час принтер печатает 70 страниц, то за 5 часов он напечатает в 5 раз больше:

70 × 5 = 350 страниц

Также, решение можно записать с помощью формулы нахождения работы. В данном случае, количество напечатанных страниц являются выполненной работой:

A = v × t = 70 × 5 = 350 страниц

A = 350 страниц

Задача 7. Принтер напечатал 350 страниц за 5 часов. С какой производительностью он работал?

Решение

Если в течении пяти часов принтер напечатал 350 страниц, то в течении часа он печатал . То есть работал с производительностью 70 страниц в час:

350 : 5 = 70 стр./ч.

Либо с помощью формулы нахождения производительности:

Задача 8. Принтер работал с производительностью 70 страниц в час и напечатал 350 страниц. Определить время работы принтера.

Решение

Выражение «работал с производительностью 70 страниц в час» означает, что в каждом часе принтер печатал по 70 страниц. И это продолжалось до тех пор, пока он не напечатал 350 страниц. Очевидно, что разделив 350 страниц по 70, мы определим время работы принтера, то есть узнаем сколько часов он работал

350 : 70 = 5 ч.

Либо с помощью формулы нахождения времени:

Задача 9. Машинистка в первый день напечатала 48 страниц рукописи, а во второй день — на 12 страниц больше, чем в первый. На всю работу в эти 2 дня она затратила 9 часов. Сколько часов работала она в каждый из этих дней, если производительность её не менялась ?

Решение

Определим сколько страниц напечатала машинистка во второй день. В условии сказано, что напечатала она на 12 страниц больше, чем в первый:

48 + 12 = 60 страниц во второй день.

Определим сколько страниц машинистка напечатала за два дня:

48 + 60 = 108 страниц за два дня.

На эту работу машинистка затратила 9 часов. Также сказано, что производительность её не менялась. Если мы разделим выполненную работу (108) на время выполнения (9), то определим производительность машинистки:

108 : 9 = 12 страниц в час.

Теперь мы можем определить сколько часов работала машинистка в каждый из двух дней. Для этого поочередно разделим выполненные работы в каждом из двух дней на производительность:

48 : 12 = 4 часа работала машинистка в первый день

60 : 12 = 5 часов работала машинистка во второй день.

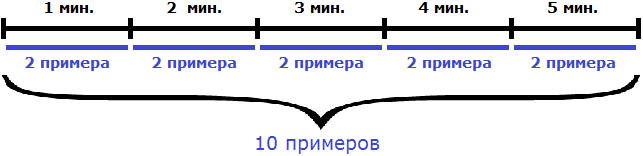
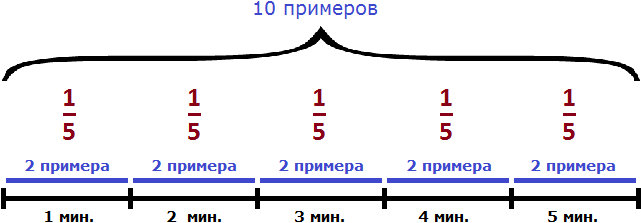
Задача 10. Джон решил 10 примеров за 5 минут. С какой производительностью он решал эти примеры?

10 примеров это выполненная Джоном работа. 5 минут — время работы. Разделим выполненную работу на время работы и определим производительность Джона:

10 : 5 = 2 примера в минуту.

Производительность Джона равна двум примерам в минуту.

Задача 11. Джон решил несколько примеров за 5 минут. С какой производительностью он решил эти примеры?

Это та же самая задача, что и предыдущая, но в ней работа не выражена каким-либо числом. Сказано лишь то, что Джон выполнил эту работу за 5 минут. Поэтому, конкретную производительность в такой задаче узнать нельзя. Но можно воспользоваться дробями. Обозначим выполненную работу через единицу. Тогда производительность работы Джона будет выражаться дробью – частью примеров, решенных за единицу времени. Если вы изучили задачи на дроби, то должны понимать о чем идёт речь.

Итак, обозначим выполненную работу через единицу:

A = 1

Мы знаем, что для нахождения производительности, выполненную работу нужно разделить на время. Время работы у нас равно пяти минутам. Поэтому, единицу делим на пять минут:

Дробь выражает часть работы, выполненную Джоном за единицу времени. Если мы вернемся к предыдущей задаче, где выполненная работа была равна десяти примерам и найдем одну пятую от этой работы, то получим 2

Выражать выполненную работу через единицу часто приходится при решении задач на совместную работу.

Задачи на совместную работу

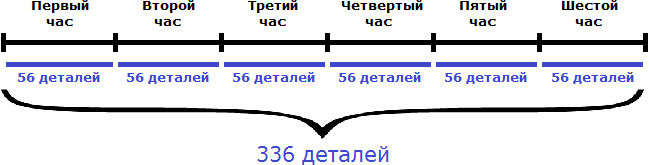
Задача 1. Первый мастер за 2 часа изготавливает 64 детали, а второй за 3 часа – 72 детали. За сколько часов они изготовят 336 деталей?

В данной задаче речь идет о совместной работе. Необходимо определить производительность обоих мастеров и найти время за которое они изготовят 336 деталей.

Для начала определим производительность первого мастера:

64 : 2 = 32 дет./час

Определим производительность второго мастера:

72 : 3 = 24 дет./час

Определим совместную производительность мастеров. Для этого сложим количество деталей, которые они изготавливают по отдельности за единицу времени. То есть сложим их производительности:

32 дет./час + 24 дет./час = 56 дет./час

Вместе за один час мастера изготавливают 56 деталей. Чтобы узнать за сколько часов они изготовят 336 деталей, нужно определить сколько раз 336 содержит по 56

336 : 56 = 6 часов

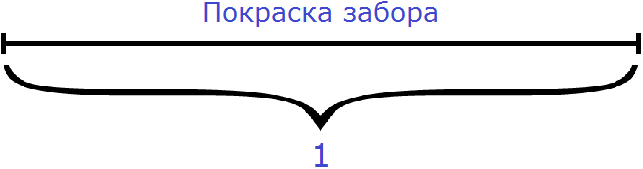
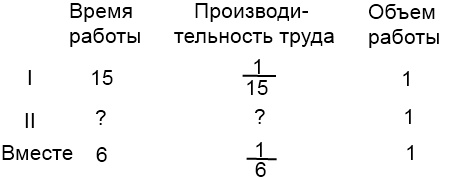
Задача 2. Первый мастер может покрасить забор за 20 минут, а второй мастер – за 30 минут. За сколько минут, работая вместе, они могут покрасить забор?

Решение

В данной задаче, в отличие от предыдущей, работа не выражена каким-либо числом. Сказано лишь то, что эту работу первый мастер может выполнить за 20 минут, а второй за 30 минут.

В такой ситуации можно воспользоваться дробями. Мы можем обозначить всю работу (покраску забора) через единицу.

Итак, обозначим работу (покраску забора) через единицу:

A = 1

Производительность первого мастера будет выражáться дробью . То есть за одну минуту он покрасит одну двадцатую часть забора. Единица это вся работа, а двадцать минут это время работы. Запишем производительность первого мастера с помощью формулы нахождения производительности:

А производительность второго мастера будет выражáться дробью . То есть за одну минуту он покрасит одну тридцатую часть забора:

Определим общую производительность мастеров. Для этого сложим дроби, выражающие производительность первого и второго мастеров:

это дробь, выражающая общую производительность обоих мастеров. То есть за одну минуту мастера вместе покрасят часть забора.

Определим время за которое мастера покрасят забор вместе. Для этого воспользуемся формулой нахождения времени: разделим выполненную работу на общую производительность мастеров. Выполненная работа у нас выражена единицей, а производительность — дробью

Ответ: работая вместе, мастера покрасят забор за 12 минут.

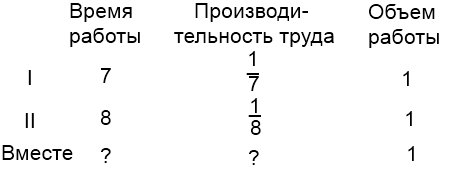
Задача 3. Первый рабочий может выполнить заказ за 8 часов, а второй за 6 часов. Два часа они работали вместе, а заканчивал работу один второй рабочий. Сколько времени потребовалось для выполнения этого заказа?

Решение

Обозначим всю работу через единицу

A = 1

Тогда первый рабочий за один час может выполнить часть работы, а второй рабочий часть работы. А вместе за один час они могут выполнить часть работы

Рабочие работали вместе два часа, поэтому умножим часть работы, выполняемую ими за один час на 2:

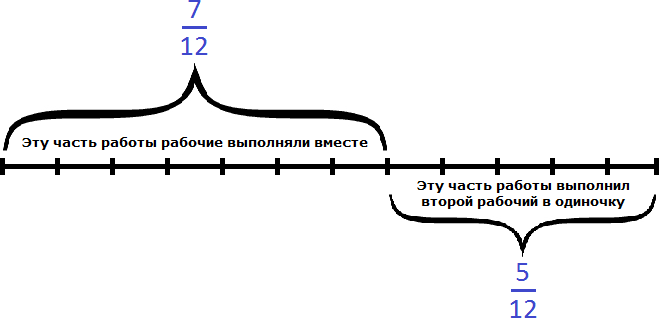
Остальную часть работы, а именно работы заканчивал один второй рабочий:

Второй рабочий за один час мог выполнить часть работы. Чтобы определить время за которое он завершил оставшуюся часть работы, воспользуемся формулой нахождения времени.

Переменная A теперь равна , переменная v —

Теперь определим общее время заказа. Первые два часа рабочие работали вместе, остальную часть работы второй рабочий выполнил за два с половиной часа, отсюда имеем 4,5 ч.

2 + 2,5 = 4,5 ч.

Ответ: для выполнения заказа потребовалось 4,5 ч.

Задача 4. Одна труба наполняет бассейн за 6 ч, а другая – за 4 ч. За
сколько часов наполняют бассейн обе трубы, работая вместе?

Решение

Обозначим работу (наполнение бассейна) через единицу

A = 1

Тогда первая труба за один час выполнит часть работы, а вторая труба — часть работы. Работая вместе за один час они выполнят часть работы:

Определим время за которое обе трубы наполняют бассейн, работая вместе:

2,4 это два целых часа и четыре десятых часа

2,4 = 2 ч + 0,4 ч

А четыре десятых часа это 24 минуты

60 мин. × 0,4 = 24 мин.

Ответ: работая вместе обе трубы наполнят бассейн за 2 ч 24 мин.

Задачи для самостоятельного решения

Задача 1. Первая бригада может выполнить некоторое задание за 12 часов, вторая – за 4 часа. За сколько часов они выполнят задание, если будут работать вместе?

Решение

Обозначим работу через единицу:

A = 1

Тогда первая бригада за один час выполнит часть работы, а вторая за один час часть работы. Их общая производительность равна сумме дробей и :

Определим время за которое обе бригады выполнят задание, работая вместе:

Ответ: обе бригады выполнят задание за 3 часа.

Задача 2. Лошадь съедает копну сена за 1 сутки, корова может съесть такую же копну за 3 суток, а овца за 6 суток. За какое время съедят эту копну лошадь, корова и овца вместе.

Решение

Работа в данном случае это съедание копны сена. Обозначим её через единицу:

A = 1

Тогда производительность лошади будет выражáться единицей, производительность коровы — дробью , производительность овцы — дробью . Их совместная производительность равна следующей сумме:

Определим время, за которое лошадь, корова и овца съедят 1 копну сена:

Ответ: лошадь, корова и овца съедят 1 копну сена за суток или 16 часов.

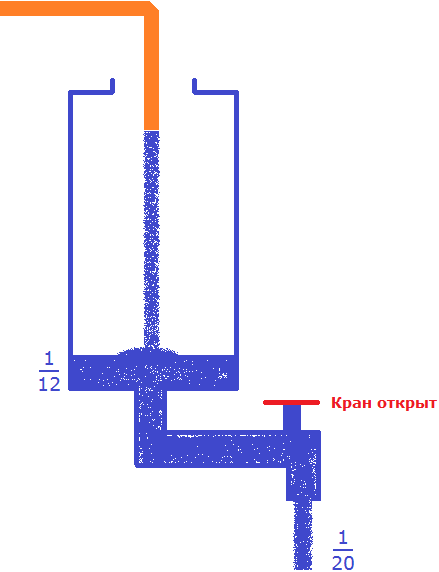
Задача 3. Сосуд наполняется шлангом за 12 мин, а полный сосуд опорожняется при открытии крана за 20 мин. За какое время наполнится пустой сосуд, если одновременно открыть кран и вливать в него воду через шланг?

Решение

Работа в данном случае это наполнение сосуда. Обозначим эту работу через единицу:

A = 1

В условии сказано, что сосуд наполняется шлангом за 12 минут. Значит в минуту будет наполняться часть сосуда. При этом сказано, что одновременно открыт кран сосуда и из него вытекает вода, которой наполняется сосуд. Вода, которая вытекает равна части сосуда, поскольку в условии сказано, что полный сосуд опорожняется за 20 минут.

В сосуд поступает воды больше, чем вытекает. Дробь больше, чем .

Несмотря на то, что часть поступающей в сосуд воды будет вытекать, с каждой минутой сосуд будет пополняться на определенную часть. Узнаем, что эта за часть. Для этого из поступающей части вычтем ту часть, которая вытекает:

Каждую минуту сосуд будет наполняться на .

Определим время за которое наполнится пустой сосуд, если одновременно открыть кран и вливать в него воду через шланг:

Ответ: если одновременно открыть кран и вливать в пустой сосуд воду через шланг, то он наполнится за 30 минут.

Задача 4. Через первую трубу бассейн можно заполнить за 20 ч, через вторую за 30 ч. Какая часть бассейна заполнится через обе трубы за 1 ч?

Решение

Работа в данном случае это заполнение бассейна. Обозначим эту работу через единицу:

A = 1

Производительность заполнения бассейна через первую трубу будет выражáться дробью , через вторую трубу — дробью . Совместная производительность будет выражáться дробью

Производительность по определению есть работа, выполненная за единицу времени. Значит дробь является ответом к задаче, поскольку нас интересовало какая часть бассейна заполнится через обе трубы за 1 час. Это можно проверить, воспользовавшись формулой нахождения работы. Переменная v у нас имеет значение , а переменная t равна единице (одному часу). Формула нахождения работы позволит нам определить какая часть работы будет выполнена за 1 час:

Ответ: за один час заполнится часть бассейна.

Задача 5. На прокладку траншеи требуется затратить 10 ч. Экскаватор проработал 8 ч, после чего ему осталось пройти 50 м. Найти общую длину траншеи.

Решение

В задаче подразумевается, что экскаватор работал с одинаковой производительностью на протяжении всей работы. На работу требовалось затратить 10 ч. Проработано было 8 ч. Значит осталось еще 2 часа. На 2 часа приходятся оставшиеся 50 метров траншеи. Если разделить 50 метров на 2, то можно определить сколько метров экскаватор прокладывает за один час:

50 : 2 = 25 м./ч

В час экскаватор прокладывал 25 метров. Работал он 10 часов. Умножим 25 на 10, мы определим общую длину траншеи:

25 × 10 = 250 м

Ответ: общая длина траншеи составляет 250 м.

Задача 6. Ванна заполняется холодной водой за 6 мин 40 с, горячей – за 8 мин. Кроме того, если из полной ванны вынуть пробку, вода вытечет за 13 мин 20 с. Сколько времени понадобится, чтобы наполнить ванну полностью, при условии, что открыты оба крана, но ванна не заткнута пробкой?.

Решение

Для удобства переведем время данное в задаче в секунды

6 мин 40 с = 400 с
8 мин = 480 с
13 мин 20 с = 800 с

Обозначим заполнение ванны через единицу:

A = 1

Производительность первого крана будет выражáться дробью , производительность второго крана — дробью . Совместная производительность обоих кранов равна сумме дробей и

Одновременно с открытыми двумя кранами, вынута пробка из ванны. Поэтому часть поступающей в ванну воды сразу выходит через слив. Эта часть будет выражáться дробью .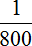

С каждой секундой ванна будет пополняться на определенную часть воды. Узнаем какая это часть. Для этого из поступающей части воды вычтем ту часть, которая вытекает через слив.

Определим сколько времени понадобится, чтобы наполнить ванну:

Ванна наполнится за 300 секунд. Поскольку задача завершена, секунды можно обратно перевести в минуты. Триста секунд это пять минут:

300 : 60 = 5 мин

Ответ: ванна заполнится за 5 мин.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Источник

ПАМЯТКА ДЛЯ РЕШЕНИЯ ЗАДАЧ ПО ФОРМУЛАМ

Формула пути

S = v• t

S – расстояние(км, дм,м)

v – скорость (км/ч, м/с, м/мин)

t – время (час, мин., сек.)

Чтобы найти расстояние, надо скорость умножить на время.

S = v• t

Чтобы найти скорость, надо расстояние разделить на время. v = S : t
Чтобы найти время, надо расстояние разделить на скорость. t =S : v

Формула стоимости

С = a • n

C – стоимость (руб.)

a – цена товара (руб.)

n – количество товара (шт., кор., л, кг, м,…)

Чтобы найти стоимость покупки, надо цену умножить на количество товара. С = a • n
Чтобы найти цену, надо стоимость разделить на количество товара. a = С : n
Чтобы найти количество товара, надо стоимость разделить на цену. n =С : a

Формула работы

A = v• t

A – работа (дет., стр., маш,…)

v – производительность (дет./час, маш./мес., стр./мин,…)

t – время (час, мин., сек.)

Чтобы найти работу, надо производительность умножить на время. A = v • t
Чтобы найти производительность, надо работу разделить на время. v = А : t
Чтобы найти время, надо работу разделить на производительность. t =А : v

Источник

Текстовые задачи на работу

В текстовых задачах на работу присутствуют такие характеристики как время и производительность – это количество работы, которую выполняют за единицу времени. Также есть такое понятие как работа – общее выполненное количество.

Эти характеристики объединятся следующей формулой:

(A = t bullet P)

где (A) – это проделанная работа, (t) – время, потраченное на её выполнение, (P) – скорость выполнения работы.

Пример №1:

Рабочие на кондитерской фабрике производят 25 коробок конфет в день. Сколько коробок конфет будет произведено через 3 дня работы?

Используем формулу производительности. Если каждый день делать по 25 коробок, а таких дня у нас 3, тогда всего будет сделано:

( A = t bullet P = 3 bullet 25 = 75 коробок)

Ответ: 75 коробок.

Пример №2:

За 5 дней работы рабочие на заводе произвели 35 деталей для автомобилей. Сколько деталей в день изготавливалось на заводе?

Для того, чтобы найти производительность, зная работу и время, нужно поделить работу на время:

(P = A : t = 35 : 5 = 7 деталей/день)

Ответ: 7 деталей в день.

ЗАДАЧИ НА ОБЩУЮ РАБОТУ

Рассмотрим ещё 2 задачи. Они похожи друг на друга, но имеют некоторые различия.

Пример №3:

Для производства инструментов нужно сделать 600 деталей. Первый завод сделает эту работу за 10 дней, а второй завод за 15. За сколько дней будут готовы все детали, если их будут делать сразу два завода?

Мы знаем работу и время производства деталей в первом заводе. Найдем их производительность:

(P_{1} = 600:10 = 60 деталей в день делает первый завод)

Также найдем производительность для второго завода:

(P_{2} = 600 : 15 = 40 деталей в день делает второй завод)

Тогда за один день два завода вместе сделают:

(P_{общ} = 60 + 40 = 100 деталей в день)

Это производительность является общей для заводов.

С такой производительностью они сделают 600 деталей за:

(t_{общ} = 600 :100 = 6 дней)

Мы узнали, за какое время заводы сделаю 600 деталей, если каждый день будут работать вместе. Запишем ответ.

Ответ: 6 дней.

Пример №4:

Первый завод сделает 600 деталей за 10 дней, а второй завод за 15. За сколько дней будут готовы 900 деталей, если их будут делать сразу два завода?

Аналогично найдем общую производительность заводов:

(P_{1} = 600:10 = 60 деталей в день делает первый завод)

(P_{2} = 600 : 15 = 40 деталей в день делает второй завод)

(P_{общ} = 60 + 40 = 100 деталей в день)

Но это еще не все. Нас спрашивают, за сколько дней будут готовы 900 деталей. Найдем это время:

(t_{общ} = 900 : 100 = 9 дней)

Ответ: 9 дней.

Источник

Тема: Работа, производительность,
время.

Цель:
ввести понятия «производительность», «выполненная работа», «время,
затраченное на работу»

Задачи:

v
установить связь между
величинами «производительность», «выполненная работа», «время, затраченное на
работу» в ходе исследовательской работы учащихся;

v
Познакомить с новым видом
задач на производительность;

v
Развивать навыки умножения
и деления многозначного числа на однозначное;

v
Формировать навыки устных
и письменных вычислений;

v
Воспитывать позитивное
отношение к труду.

Оборудование: учебник, карточки для индивидуальной работы, табличка с пословицей –
эпиграфом урока, карточки для введения в новую тему, песочные часы, таблица,
стикеры — цветочки.

Ход урока

I. Организационный момент.

У.- Начинается урок,

Он пойдёт ребятам впрок,

Постарайтесь всё понять,

Учитесь тайны открывать,

Ответы полные давать,

Чтоб за работу получать

Только лишь отметку «пять»!

Слово учителя: Какую работу мы можем выполнить на
сегодняшнем уроке математики? Решать задачи, думать над примерами, считать,
записывать условие задачи и т.д.

— Надо нам сегодня поработать!

— А какие пословицы о труде вы знаете?

· Не спеши языком, торопись делом.

· Дело мастера боится.

· Без труда не вытащишь рыбку из пруда.

· Рабочие руки не знают скуки.

— Эпиграфом нашего урока будет пословица. Прочитайте:


	ВСЯКОЕ УМЕНИЕ ТРУДОМ ДАЁТСЯ

— Объясните значение
пословицы.

II. Актуализация опорных знаний.

1.Индивидуальная работа. Умножение и деление многозначного числа на
однозначное. Решение примеров на карточках.

Учащиеся решают примеры и делают проверку. (Взаимопроверка)

Вопросы после проверки:

— Какую работу выполняли? Кто быстрее справился? Почему?

2.Работа с классом. «Математическая разминка»

— Сколько богатырей у дядьки Черномора?

— Сколько месяцев в году, кроме летних?

— Сколько граммов в 4,5 килограммах?

— Количество букв в названии нашей страны увеличить в 400 раз.

— Мальчик лёг спать в 9 часов вечера, а смог заснуть только через три
часа. Который час показывали часы?

— Количество месяцев зимы увеличьте в 320 раз.

— Умножьте количество букв в детском имени Александра на число слогов в
нём же.

3. Повторение устных приёмов умножения и деления чисел, оканчивающихся
нулями. Игра «Кто быстрей?» (Ответы спрятаны под звездой)

140 · 5 = 700 45 000 · 2 = 90 000
700 · 6 = 4200

800 · 9 = 7200 8 000 : 4 = 2 000
6 300 : 7 = 900

— Как решали данные примеры?

4. Математический диктант.

Чему равна сумма 120 и произведения чисел 30 и 5?

Найдите частное чисел 250 и 2.

Увеличьте 460 в 2 раза.

Увеличьте 380 на 200.

Сумма чисел 800, первое слагаемое 320. Найдите второе слагаемое.

Найдите произведение чисел 320 и 3.

Запишите частное чисел 4 800 и 4.

Запишите число, меньшее 1 800 в два раза.

При проверке объяснить способ вычисления.

III. Объяснение нового материала

1. Подготовка к восприятию нового материала

— Вот песочные часы, песок высыпается в нижнюю часть за 1 минуту.
Перед вами карточки с заданиями. Сколько заданий вы успеете выполнить за одну
минуту?

Вычисли, чему равен периметр квадрата со
стороной 60 см.
Чему равен периметр прямоугольника со
сторонами 8 см и 7 см?
Вычисли периметр треугольника со
сторонами 30 см, 45 см, 57 см.
Вычисли длину стороны квадрата, периметр
которого равен 48 см.
Найди длину прямоугольника, периметр
которого равен 30 см и ширина равна 5 см.
Вычисли площадь прямоугольника со
сторонами 7 см и 4 см.
Чему равна ширина прямоугольника, если
площадь его 45 кв. см, а длина равна 5 см?
Длина прямоугольника – 54 мм, а ширина –
на 24 мм меньше. Вычисли периметр и площадь прямоугольника.

— Минута закончилась. Переверните листок, проверьте правильность
решения. Поставьте + или – за решение.

— Сколько заданий за 1 минуту выполнили?

— А сколько бы вы выполнили за 40 минут, если бы решали весь урок
аналогичные задания? (3 · 40 = 120 з., 4 · 40 = 160 з. и т.д.)

— Что такое 40 минут? (Время выполнения задания)

— Что обозначает число 3? (Количество заданий, выполняемых за

1 минуту)

— А что обозначает число 120? ( Количество заданий, которое можно
выполнить за урок)

2. «Открытие» детьми нового знания

— Как вы думаете, над чем сегодня предстоит работать? ( Будем
учиться находить время работы, количество заданий, и всю работу)

Учитель:

— В математике существуют понятия: (карточки)


			Время, затраченное на работу

— А как вы понимаете слово «производительность»? (это объём работы,
выполненный за единицу времени)

— В
случае с заданиями на карточках, что будет являться производительностью труда?
(количество заданий, которые выполнили за 1 мин.)

— Одинаковой ли была производительность у
каждого из вас? (Разная)

— Когда
умножали производительность своего труда на время 40 мин, что вы получили? (Количество
заданий, которое можем выполнить за весь урок, объём всей работы)

— Почему объём работы оказался разным у разных учеников? (Потому что
разная производительность труда)

3. Сообщение темы и цели урока. Работа по таблице.

4. Знакомство с единицами измерения производительности.

— Производительность ткацкого станка 9м/ч. — «Девять метров в час». Это
значит, что за час можно изготовить 9 метров ковра.

ΙV. Первичное закрепление.

1.
Нахождение
производительности. Задачи

Учащиеся чертят таблицу в тетрадях

А) Бригада посадила 1200 деревьев за 20 дней.

Б) Бассейн вместимостью 18 000 л наполнился через трубу за 6 ч.

В) 360 т кирпича машина перевезла за 60 рейсов.

Г) Мастерская переплела 600 книг за 10 дней.

Д) Комбайн собрал 8000 ц зерна за 10 дней.

	Производительность	Время, затраченное на работу	Выполненная работа
1)	*60 деревьев в день*	20 дней	1200 деревьев
2)	*3 000 л/ч*	6 часов	18 000 л
3)	*6 т за рейс*	60 рейсов	360 т
4)	*6 книг в день*	10 дней	600 книг
5)	*800 ц за день*	10 дней	8 000 ц

Вывод:
Чтобы найти производительность, надо выполненную работу разделить на время,
затраченное на работу

— Глядя в таблицу, скажите, в каких единицах измеряется
производительность?

2. Работа с правилом и формулой нахождения производительности.

Установка на запоминание правила и формулы.

Физминутка

Мы сейчас бревно распилим.

Пилим, пилим, пилим, пилим.

Мы сейчас дрова расколем.

Колем, колем, колем, колем.

Раз-два. Раз-два!

Будут на зиму дрова.

3. Сравнение задач. Задача «Рабочий в час изготавливает 20
деталей. Сколько деталей он сделает за 6 часов?»

Анализ задачи 1):

— Что нужно узнать в задаче? Сколько деталей изготовит рабочий за 6
часов, т.е. объём выполненной работы

— Что для этого надо знать? Сколько деталей он делает за час и время
работы

— Известно, сколько деталей он делает за час? (производительность 20
деталей в час)

— Известно время, затраченное на работу? 6 часов

— Как найти объём выполненной работы?

Решение: 20 · 6 = 120 деталей

Ответ: 120 деталей изготовят за 6 часов.

Анализ задачи 2): «Рабочий за 7 часов изготавливает 175 деталей.
Сколько деталей рабочий делает за час?»

— Что известно в задаче? объём выполненной работы – 175 деталей и
время работы – 7 ч

— Что нужно узнать? Производительность

— Как найдёте?

Решение: 175 : 7 = 25деталей в час

Ответ: 25 деталей в час изготавливал рабочий.

Анализ задачи 3): «Рабочий за час изготавливает 23 детали.
Сколько времени он потратил, чтобы изготовить 184 детали?»

— Что нужно узнать в задаче? Время, затраченное на работу

— Что для этого надо знать? Выполненную работу и производительность

— Известен объём работы? Известна производительность?

— Как найти время, затраченное на работу? Выполненную работу
разделить на производительность

Решение: 184 : 23 = 8 ч

Ответ: за 8 часов

— Сравнить задачи.

— Повторить, как найти производительность? Объём выполненной работы?
Время, затраченное на работу?

V. Закрепление пройденного материала.

Задание повышенной сложности.

— решить задачу при помощи графа.

«Слесарь, штукатур, водитель, маляр, крановщик, токарь и плотник были в
отпуске в разное время. Отпуск маляра был позже отпуска слесаря, отпуск
которого был позже отпуска плотника. Отпуск токаря был раньше отпуска
крановщика, но позже отпуска штукатура. Отпуск водителя был раньше отпуска
плотника, но позже отпуска крановщика. Кто из рабочих был в отпуске раньше, кто
позже?»

Рекомендации к решению.

Изображаем точками названия профессий людей. Учащиеся
анализируют условие задачи. Далее
нужно выбрать одно из отношений «раньше» или «позже». Например,
выбрали отношение «раньше». Это слово записываем около
рисунка. Читаем задачу снова, заменяя предложение со словом «позже»
предложением со словом «раньше» и показываем это на рисунке с помощью
стрелки: ведем стрелку от одного рабочего к другому, который ушёл в отпуск
раньше.

раньше

Ответ: Раньше всех пошёл в отпуск штукатур, позже всех – маляр.

VI. Рефлексия.

— С какими новыми понятиями познакомились на уроке?

— Какая производительность была у нас на уроке? Скажите одним словом.

— Можете теперь сказать, что всякое умение трудом даётся?

Источник

Типичные задачи на совместную работу в 6 классе

1) Двое рабочих, работая вместе, выполняют некоторую работу за 6 часов. Один из них, работая самостоятельно, может выполнить эту работу за 15 часов. За сколько часов может выполнить эту работу другой рабочий?

В отличие от всех других типов задач, задачи на совместную работу начинаются с того, что всю работу (все задание, весь бассейн, все поле — то, о чем идет речь в задаче) принимаем за единицу. То есть объем работы в этом случае равен единице. Чтобы найти объем работы, надо производительность труда умножить на время работы. Соответственно, чтобы найти производительность труда (часть работы, выполненную за определенную единицу времени), надо объем работы разделить на время работы: 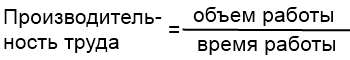Решение задач на совместную работу упрощается, если условие оформить в виде таблицы.

Перейдем с решению нашей задачи.

Решение.

Примем всю работу за 1.

Чтобы найти производительность труда второго рабочего, из производительности труда совместной работы вычтем производительность труда первого рабочего:

$[1)frac{{{1^{backslash 5}}}}{6} - {frac{1}{{15}}^{backslash 2}} = frac{{5 - 2}}{{30}} = frac{3}{{30}} = frac{1}{{10}}]$

Такую часть работы в 1 час выполняет второй рабочий.

Зная производительность труда второго рабочего и объем работы, можем найти время, за которое он может выполнить работу самостоятельно. Чтобы найти время работы, надо объем работы разделить на производительность труда:

$[2)1:frac{1}{{10}} = 1 cdot frac{{10}}{1} = 10]$

Значит, второй рабочий, работая отдельно, может выполнить работу за 10 часов.

Ответ: за 10 часов.

2) Через одну трубу бассейн наполняется за 7 часов, а через другую опустошается за 8 часов. За какое время бассейн будет наполнен, если открыть обе трубы?

Решение.

Примем весь бассейн за 1.

Сначала найдем производительность труда совместной работы обеих труб за один час. Поскольку одна труба бассейн наполняет, а другая — опустошает, производительность совместной работы равна разности производительности первой и второй труб:

$[1)frac{{{1^{backslash 8}}}}{7} - frac{{{1^{backslash 7}}}}{8} = frac{{8 - 7}}{{56}} = frac{1}{{56}}]$

Теперь найдем время, за которое бассейн будет наполнен при открытии обеих труб одновременно. Чтобы найти время работы, надо объем работы разделить на производительность труда:

$[2)1:frac{1}{{56}} = 1 cdot frac{{56}}{1} = 56]$

Таким образом, за 56 часов совместной работы обеих труб бассейн будет наполнен.

Ответ: за 56 часов.

Источник

Тип урока: ОНЗ.

Основные цели:

cформировать представление о величине «производительность»;
выявить зависимость между величинами: объемом выполненной работы (А), производительностью (v) и временем (t), формировать умение строить формулы;
формировать умение находить по формуле работы v и t;
формировать умение использовать формулу работы для решения задач, тренировать вычислительные навыки.

Планируемые результаты: знать формулу работы A = v · t, устанавливать взаимосвязь между величинами, уметь использовать их для решения текстовых задач.

Мыслительные операции, необходимые на этапе проектирования: анализ, синтез, сравнение, обобщение, классификация.

Ход урока

1. Мотивация к учебной деятельности

Цель:

создать условия для возникновения у учащихся внутренней потребности включения в деятельность;
актуализировать требования к ученику со стороны учебной деятельности;
установить тематические рамки урока: работа с формулами.

Организация учебного процесса на этапе 1:

— Начинаем урок математики. Проверьте, все ли готовы к уроку.

Презентация.

(Слайд) Китайский философ Конфуций сказал:

Послушайте — и Вы забудете,
Посмотрите — и Вы запомните,
Сделайте – и Вы поймёте.

— Что это значит, как вы будете работать на уроке? (Будем не просто слушать, и смотреть, а сами открывать новые знания.)

— Действительно, у нас урок открытия новых знаний.

— Желаю вам успешной работы на уроке!

— Начнём работу с повторения.

2. Актуализация знаний и фиксация затруднения в пробном учебном действии

Цель:

организовать актуализацию изученных формул (площади, стоимости, пути). Зафиксировать взаимосвязь между этими величинами вербально (в речи) и знаково (эталон) и обобщить их.
организовать актуализацию мыслительных операций: анализ, сравнение, обобщение и познавательных процессов, достаточных для построения нового знания.
мотивировать к пробному действию и его самостоятельному выполнению и обоснованию.
предъявить индивидуальное задание для пробного действия и проанализировать его с целью выявления нового учебного содержания.
организовать фиксацию образовательной цели и темы урока.
организовать выполнение пробного действия и фиксацию затруднения.
организовать анализ полученных ответов и зафиксировать индивидуальные затруднения в выполнении пробного действия или его обосновании.

Организация учебного процесса на этапе 2:

(Слайд):

— Подберите «ключики» к новому знанию.

1. Повторение известных формул.

У каждого ученика набор карточек с известными формулами с пропусками.

— Восстановите формулы.

Учащиеся выполняют задание на карточках.

— Проверьте свои работы. (Слайд)

— Прочтите получившиеся формулы? (Чтобы найти …, надо…).

— Где вы используете знание формул? (Когда решаем задачи.)

— Как вы думаете, какое теперь задание я вам предложу? (Решить задачу.)

2. Решение задач.

Учащиеся работают в тетрадях, с фронтальной проверкой.

— Я буду читать задачу, а вы выбираете и записываете формулу, устанавливающую взаимосвязь между величинами, о которых говорится в задачи и решаете задачу.

— На что нужно обратить внимание при записи решения? (На обозначение величин.)

1) Длина прямоугольника равна 7 дм, а ширина – 3 дм. Какова его площадь?

(S = a · b, чтобы найти площадь прямоугольника, надо длину умножить на ширину: 7 · 3 = 21 дм².)

2) Цена пирожка 9 рублей. Сколько стоят 5 пирожков? (C = a · n , чтобы найти стоимость, нужно цену умножить на количество: 9 · 5 = 45 руб.)

3) Пешеход прошел 20 км за 4 часа. С какой скоростью он шел? (v= s : t, чтобы найти скорость, надо пройденный путь разделить на время движения: 20 : 4 = 5 км/ч.)

— Что вы повторили? (Формулы, решение задач на стоимость, площадь и движение.)

3) Пробное действие

— А сейчас я вам предложу ещё одну задачу. Когда я над ней работала, мне вспомнился замечательный праздник проводов зимы. Как он называется? Что является символом Масленицы? (Слайд)

На масленичной неделе были горы вкусных блинов и на завтрак, и на обед, и на ужин.

«На завтрак мама выпекала 3 блина в минуту. Сколько блинов приготовила мама, работая 20 минут?»

— Что нового в задании?

Учащиеся выполняют задание самостоятельно.

— У кого нет ответа?

— Что вы не смогли сделать?

— Какие ответы получили?

Если среди ответов будет правильный, предложить учащимся, которые их получили показать, какой формулой они пользовались при ответе на вопрос задачи.

— Что вы не можете сделать? (Мы не можем обосновать свой ответ, не можем указать формулу, которой пользовались при решении задачи.)
— С чем вы столкнулись? (С затруднением.)

— Слово «трудность» не должно существовать для творческого ума. Препятствия не бесполезны для ума.

3. Выявление места и причины затруднения

Цель:

организовать восстановление выполненных операций и фиксацию (вербальную и знаковую) места – шага, операции, где возникло затруднение.
организовать соотнесение действий учащихся с используемым способом (алгоритмом, понятием и т.д.) и на этой основе организовать выявление и фиксирование во внешней речи причины затруднения – тех конкретных знаний, умений или способностей, которых недостаёт для решения исходной задачи такого класса или типа.

Организация учебного процесса на этапе 3:

— Давайте подумаем.

— Что вы должны были сделать? (Мы должны были определить сколько блинов выпечет мама за 20 минут, должны были решить задачу.)

— Что вы использовали при решении задачи?

— Где возникло затруднение? (При выборе формулы.)

— Чем эта задача отличается от тех, которые вы решали в начале урока? (Раньше мы решали задачи с известными нам величинами, а в этой задаче не все величины нам знакомы, мы знаем только время.)

— Почему возникло затруднение? (Новые величины в задаче, нет формулы.)

4. Построение проекта выхода из затруднения

Цель:

В коммуникативной форме организовать построение учащимися проекта будущих учебных действий:

уточнение цели проекта (целью всегда являются устранение возникшего затруднения);
выбор способа (дополнение или уточнение);
определение средств (алгоритмы, модели, учебник и т.д.);
построение плана достижения цели.

Организация учебного процесса на этапе 4:

— Как можно назвать процесс приготовления блинов или другой продукции? (Работа.)

— Итак, сегодня мы будем говорить о работе.

— Какую цель поставим перед собой? (Узнать о новых величинах, ввести обозначения этих величин и установить взаимосвязь между ними, т.е. построить формулу.)

— Давайте составим план работы (Слайд):

1. Найти величины, описывающие процесс работы.

2. Обозначить величины буквами.

3. Установить взаимосвязь между величинами, записать формулу.

— Формулу чего вы будете открывать? (Формулу работы.)

— Сформулируйте тему урока. (Формула работы.)

5. Реализация построенного проекта

Цель:

организовать коммуникативное взаимодействие с целью реализации построенного проекта, направленного на приобретение недостающих знаний: построения формулы работы.
организовать фиксацию построенного способа действия в речи и знаково (с помощью эталона).
организовать решение исходной задачи в случае использования на этапе проектирования другого задания и зафиксировать преодоление затруднения.
организовать уточнение общего характера нового знания.

Организация учебного процесса на этапе 5:

— На завтрак мама выпекала 3 блина в минуту. Как вы думаете, о какой величине идет речь? (О скорости работы.)

— Докажите, что это величина? (Можно сравнить, выполнять различные операции.)

Скорость работы называют производительностью и обозначают буквой v.

— Что еще известно в задаче? (Время работы 20 минут.)

— О какой величине идет речь? (О времени.)

— Какой буквой обозначается эта величина? (t)

— Запишите в таблицу.

— Что нужно узнать в задаче? (Количество всех блинов, т.е. какую работу выполнила мама.)

— Докажите, что работа величина? (Можно сравнить, выполнять различные операции.)

— Эта величина обозначается буквой А.

— Как найти количество блинов, которые испекла мама за 20 минут, если известно, что за 1 минуту мама выпекает 3 блина? (Надо 3 блина умножить на 20 минут: 3 · 20 = 60 (б.) испекла мама.)

Дети выполняют запись на листах.

— Какую величину находили? (Работу.)

— Как находили? (Производительность работы умножили на время.)

— Запишите формулу зависимости этих величин.

Учащиеся работают на листах. (Слайд)

— Справились вы с поставленной целью? (Да.)

— Докажите? (Мы узнали о величинах, установили их взаимосвязь, построили формулу.)

— Все ли формулы открыты на доске? (Нет.)

— Чтобы их открыть нужно отдохнуть.

Физминутка

— Какие формулы можно вывести пользуясь правилом нахождения неизвестного множителя? (Слайд)

— Как найти производительность труда? (Чтобы найти производительность труда нужно работу разделить на время.)

— Как найти время работы? (Чтобы найти время нужно работу разделить на производительность труда.)

— Запишите формулы на листочке. Сравните с эталоном на доске.

— Как называется работа, выполненная за единицу времени. (Производительность труда.)

— Как найти работу? Производительность? Время работы?

— Где вы можем использовать полученное знание? (При решении задач.)

— Какие задачи вы теперь сможете решать? (Задачи на работу.)

6. Первичное закрепление во внешней речи

Цель:

организовать усвоение детьми новой формулы и работы с ней при решении типовых задач с их проговариванием во внешней речи (фронтально, в парах или группах).

Организация учебного процесса на этапе 6:

— С затруднением справились, цель достигли. Теперь будем тренироваться в использовании формул.

— Откройте учебник стр. 44 № 1 (а, б).

— Какое задание нужно выполнить? (Объяснить смысл предложений.)

а) Вася каждый час съедает 3 мороженых.

— А сколько мороженых Вася съест за 2 часа? (3 · 2 = 6 (мор.) Какую величину находили? (Работу.)

б) Оля за 1 минуту лепит 2 штуки пельменей.

— Дополните условие и поставьте вопрос к задаче.

№ 2.

— Какое задание будете выполнять? (Решать задачу)

— Прочтите задачу.

— Проанализируйте условие.

— Что это значит? (Установить известные величины, что дано, что надо найти.)

Один из учащихся анализирует условие задачи.

— Как ответить на вопрос задачи? (Надо производительность труда умножить на время.)

t ч	2	4	6	7	9	t
А дет.

v = 8 дет./ч

А = ___________

— Найдите работу, выполненную мастером за 6 часов, 7 часов.

Учащиеся работают в парах.

(Слайд)

t ч	2	4	6	7	9	t
А дет.	16	32	48	56	72	8 · t

v = 8 дет./ч

А = 8 t

7. Самостоятельная работа с самопроверкой по эталону

Цель:

организовать самостоятельное выполнение учащимися задания на новый способ действия: решение задач с помощью формулы работы;
организовать самопроверку на основе сопоставления с эталоном.

По результатам выполнения самостоятельной работы организовать рефлексию усвоения нового способа действия.

Организация учебного процесса на этапе 7:

Задача на листах «Аспар и Георгий с удовольствием ели вкусные блины. Аспар за 1 минуту может съесть 3 блина, а Георгий за 1 минуту – 2 блина. Кто из мальчиков съест больше блинов за 5 минут и на сколько?»

— Заполните самостоятельно таблицу и решите задачу, обратите внимание на обозначение величин.

— Проверяем. Какой формулой пользовались? (Формулой работы)

— Как решали?

1). 3*5=15 (б.) – съел Аспар.

2). 2*5=10 (б.) – съел Георгий.

3). 15-10=5 (б.) – Аспар съел больше, чем Георгий.

— Кто получил такой результат?

— Кто допустил ошибку?

— Почему допустили ошибку?

— Зафиксируйте результат самопроверки с помощью знаков «+» или «?».

— Исправьте ошибки.

8. Включение в систему знаний и повторение

Цель:

тренировать способность к к решению задач по формуле работы.
совершенствовать навык умножения многозначных чисел.

Организация учебного процесса на этапе 8:

— Где сможем применить полученное знание? (При решении задач…)

Приложение.

— Мне хочется узнать, с какой производительностью вы умеете работать. Решим примеры за единицу времени – 1 минуту. (Слайд)

850 : 5=
37 · 3 =
360 — 180 =
720 : 6 =
46 20 =
91 : 7 =
590 + 160 =
5500 : 100 =
250 · 30 =
148 : 2 =

— Сколько примеров решили?

— За какое время вы решили примеры?

— Как называется эта величина? (Производительность)

— Она у всех одинаковая? (Нет)

— А сколько примеров мог бы решить каждый из вас, если бы работал весь урок, 40 минут?

— Как называется величина, которую необходимо найти? (Работа)

— Она у всех будет одинаковая? Почему?

9. Рефлексия учебной деятельности на уроке

Цель:

организовать фиксацию нового содержания, изученного на уроке;
организовать рефлексивный анализ учебной деятельности с точки зрения выполнения требований, известных учащимся;
организовать оценивание учащимися собственной деятельности на уроке;
организовать фиксацию неразрешённых затруднений на уроке как направления будущей учебной деятельности;
организовать обсуждение и запись домашнего задания.

Организация учебного процесса на этапе 9:

— По окончании любой деятельности нужно подвести … (Итог работы.)

— Какие цели вы ставили на уроке? (Узнать о новых величинах, ввести обозначения этих величин и установить взаимосвязь между ними, т.е. построить формулу работы.)

— Что явилось итогом работы? (Формулы.)

— Достигли вы цели? Докажите.

— Кто сегодня смог сам вывести формулы?

— Вы сами открыли замочек и… ряд изученных формул пополнился.

— У кого были трудности?

— В чем причина?

— Проанализируйте свою работу на уроке.

— Следует ли еще тренироваться?

Источник

9 февраля.

Классная работа.

1 команда — 9 шаблонов 2 команда – 12 шаблонов 3 команда – 15 шаблонов

Тема урока : «Работа. Время. Производительность».

Сформулируйте цель урока. Продолжите …

Сегодня мы узнаем ….

Сегодня мы будем учиться…

Чтобы найти производительность, надо всю выполненную работу разделить на время. v = А : t

Чтобы найти время работы, надо работу разделить на производительность. t = А : v

Выполненная работа равна производительности, умноженной на время работы. А= v · t

Самостоятельная работа Определите: а) производительность кондитера, если он за 3 часа сделал 150 кг конфет; б)производительность фасовщика, если он за 2 дня сделал 180 подарков;

Самостоятельная работа

150 кг

50 кг

180 п.

90 п.

3 часа

2 дня

Оцените свои умения — Да, я умею решать задачи пользуясь формулой работы — Не хватает уверенности в решении задач с помощью формул — Пока я затрудняюсь в решении задач с помощью формул