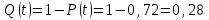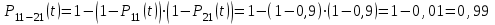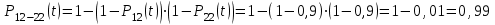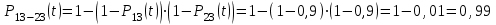Какова вероятность безотказной работы системы в начальный момент времени

1. Показатели безотказности

1.1. Вероятность
безотказной работы
– вероятность того, что в пределах
заданной наработки t
отказ не возникнет.

,

где N_р
– число работоспособных объектов на
момент t;

N – общее число наблюдаемых
объектов;

n(t) – число объектов,
отказавших на момент t от начала испытаний
или эксплуатации.

Вероятность
безотказной работы умень­­шается
с увеличением времени работы или
наработки объекта. Зависимость вероятности
безотказной работы от времени
характеризуется кривой убыли ресурса
объ­екта, пример которой приведен на
рисунке 9.

В начальный момент времени
для работоспособного объекта вероятность
его безотказной работы равна единице
(100 %). По мере работы объекта эта вероятность
снижается и стремится к нулю.

Вероятность отказа
характеризуется вероятностью возникновения
отказа на момент времени t
:

,

где
n(t) – число объектов, отказавших на
момент t от начала испытаний или
эксплуатации;

N – общее число наблюдаемых объектов.

Вероятность возникновения
отказа объекта возрастает с увеличе­нием
срока эксплуатации или наработки.

Пример зависимости вероятности
возникновения отказа от времени показан
на рисунке 10. Для работоспособного
объекта в начальный момент времени
вероятность отказа близка к нулю. Для
того, чтобы отказ проявился, объекту
необходимо начать работать, при этом
вероятность отказа увеличивается с
увеличением времени и стремится к
единице.

Вероятность отказа может
быть также охарактеризована плотностью
вероятности отказа

или,

где
– число отказов за промежуток времени
Δt;

N – общее число наблюдаемых
объектов.

Пример
1. После 500 часов
наработки из 56 агрегатов, поставленных
на эксплуатацию, в работоспособном
состоянии оказалось 43 агрегата. Определить
вероятность безотказной работы агрегата
в течение 500 час.

Решение:

Используем формулу для определения
вероятности безотказной работы объекта

.

Вероятность безотказной
работы агрегата в течение 500 часов
составляет 76,8 %.

Пример
2. Для предыдущего
примера определить вероятность отказа
агрегат за 500 часов работы.

Решение:

Используем формулу для вероятности
отказа

или

.

Таким образом, вероятность
отказа агрегата за 500 часов составляет
23,2 %.

При определении вероятности
безотказной работы и вероятности отказов
широко используются две основных теоремы
для определения вероятности случайного
события.

1. Вероятность появления
одного из двух несовместных событий
равна сумме вероятности этих событий:

,

где A,
B
– несовместные события.

2. Вероятность совместного
появления нескольких независимых
событий равна произведению вероятностей
этих событий:

.

Первая теорема используется
для нахождения вероятности отказа при
возможности у объекта нескольких видов
несовместных отказов. С использованием
второй теоремы определяют вероятность
безотказной работы объекта, состоящего
из многих элементов, вероятность
безотказной работы которых известна.

Пример
3. Система состоит
их 4-х агрегатов. Надежность каждого
агрегата в течение времени t
характеризуется вероятностью безотказной
работы 90 %. Найти вероятность безотказной
работы системы в течение времени t
при условии независимости отказов
агрегатов.

Решение:

Используем теорему вероятности
совместного появления работоспособного
состояния всех агрегатов:

.

Следовательно, вероятность
безотказной работы системы в течение
времени t
равна 65,6 %.

Пример
4. В составе
агрегата имеются 5 узлов. Вероятность
отказа каждого узла в течение времени
t
составляет 5 %. Отказы узлов несовместны.
Определить вероятность отказа агрегата.

Решение:

Используем теорему для
вероятности хотя бы одного из нескольких
несовместных событий:

.

Таким образом, вероятность
отказа агрегата в течение времени t
составляет 25 %.

2. Интенсивность
отказов –
характеризует скорость возникновения
отказов объекта в различные моменты
времени его работы:

,

где n(t)
– число отказов за промежуток времени
t;

N_р
– число работоспособных объектов на
момент t.

Интенсивность отказов может быть найдена
теоретически

,

где f(t) – функция плотности
вероятности наработки до отказа;

P(t) – вероятность безотказной
работы,

.

Плотность распределения
f(t) наработки до отказа может быть также
определена по вероятности отказа

или.

Вероятность безотказной работы связана
с интенсивностью отказов одним из
основных уравнений теории надежности:

.

В описанных способах оценки
безотказности до первого отказа отказы
не различаются по тяжести их последствий.
В большинстве случаев при разработке
объекта необходимо установить критерий
отказа изделия по экономическим
соображением, исчерпанию ресурса или
другим характеристикам.

Критерием
отказа называют
признак или совокупность признаков
неработоспособного состояния объекта,
установленных в нормативно-технической
или конструкторской документации.

3. Средняя
наработка на отказ
– это отношение наработки восстанавливаемого
объекта к математическому ожиданию
числа его отказов в течение этой
наработки:

,

где N – общее число объектов,
поставленных на испытания или в
эксплуатацию;

t _i
– наработка i-того объекта;

m _i
– число отказов i-того объекта за весь
наблюдаемый период.

Средняя наработка на отказ
используется для характеристики
восстанавливаемых объектов.

4.
Средняя наработка до отказа –
математическое ожидание наработки
объекта до первого отказа

или,

где N_pi
– число работоспособных объектов на
интервале наработки t_i–t_i+1
;

N – общее число наблюдаемых объектов;

t
= t_i+1–t_i
– интервал времени;

k – число рассматриваемых
интервалов наработки.

Среднюю наработку до отказа можно также
определить иначе

,

где t_i
– наработка до отказа i-того объекта;

n – число объектов.

Показатель Т_ср
используется для характеристики
надежности невосстанавливаемых объектов.

5.
Средняя
наработка между отказами
– математическое ожидание наработки
объекта от окончания восстановления
его работоспособного состояния после
отказа до возникновения следующего
отказа.

Вычисляется как отношение суммарной
наработки объекта между отказами за
рассматриваемый период к числу отказов
за тот же период:

.

Показатели безотказности определяют
на разных стадиях работы объекта с целью
его совершенствования и с целью контроля
нормируемых значений при эксплуатации.

Соседние файлы в папке НАДЕЖНОСТЬ_3_ГРАДИРНИ

• #

  21.03.20168.84 Mб51НАДЕЖНОСТЬ_Ушаков_ГРАДИРНИ.pdf

• #
• #
• #

  21.03.201616.52 Mб54НАДЕЖНОСТЬ_Эдельман_ГРАДИРНИ.pdf
• #

С этим файлом связано 2 файл(ов). Среди них: Практическое занятие расходометры.docx, Практическое занятие монтаж Гамма — 7.docx.
Показать все связанные файлы

Подборка по базе: Курсовая работа по Административному праву.docx, Контрольная работа Институциональная экономика Халилова Эмиллаdo, Практическая работа 3.docx, контрольная работа №3 Давление твёрдых тел, жидкостей и газов.do, Исследовательская работа по теме _Эффективность 2 х схем лечения, Контрольная работа №4 8 кл.docx, Итоговая работа №4.docx, Конфликтология и медиация. Практическая работа Иванова А.А.docx, Практическая работа по теме Законодательство по ИБ РФ.docx, Практическая работа №2 Литус Елена Петровна.docx

_{Практическая работа № 60 «Расчет надежности сложных систем»}
Цель: научить студентов определять показатели надежности объектов, представляющих сложные системы.
Задачи обучения:

• ознакомить с методами резервирования;
• привить навыки построения структуры сложной системы;
• научить рассчитывать показатели надежности системы без резервирования;
• научить рассчитывать показатели надежности системы с резервированием.

Задания и методические указания к их выполнению (алгоритм, форма, сроки отчетности, критерии оценивания):

Пример 6.1. Определить вероятность безотказной работы и вероятность отказа основной системы, состоящей из пяти элементов, если вероятности безотказной работы элементов равны P₁(t)=0,98, P₂(t)=0,97, P₃(t)=0,99, P₄(t)=0,98, P₅(t)=0,96.

Решение: вероятность безотказной работы системыP_с(t) определяем по формуле (3.1):

,

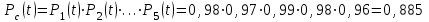
вероятность отказа Q_c(t) системы определяется по формуле (3.5):

.

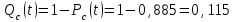
Ответ: .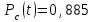

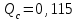
Пример 6.2. Определить среднее время безотказной работы системы, если система состоит из трех элементов, среднее время безотказной работы которых равны 400, 200 и 500 часов, закон распределения – экспоненциальный.

Решение: Определим интенсивности отказов элементов по формуле (2.11)

1/час; 1/час;

1/час.

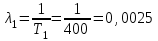
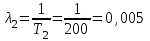
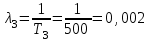
Интенсивность отказа системы определяем по формуле (3.7)

1/час.

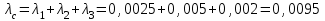
Наработку до отказа системы рассчитаем по формуле (3.8)

час.

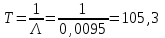
Ответ: 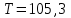час.

Пример 6.3. Система состоит из трех элементов, вероятность безотказной работы которых в течении 100 часов равны Р₁(100) = 0,95; Р₁(100) = 0,99; Р₃(100) = 0,97. Найти среднее время безотказной работы системы, закон распределения – экспоненциальный.

Решение: Определим вероятность безотказной работы системы

.

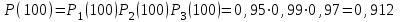
Выразим интенсивность отказа системы из формулы (3.6)

.

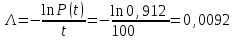
Среднее время безотказной работы системы определяем по формуле (3.8)

час.

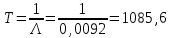
Ответ: 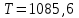час.

Пример 6.4. Система состоит из 6000 элементов, средняя интенсивность отказов которых _ср=5,4*10^-7 1/час. Определить вероятность безотказной работы, вероятность отказа, плотность вероятности времени безотказной работы за время 100 часов, и среднее время безотказной работы.

Решение: Интенсивность отказов системы определяем по формуле (3.7)

.

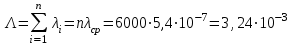
Вероятность безотказной работы рассчитаем по формуле (3.6)

,

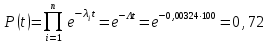
Вероятность отказа системы

Наработка до отказа системы

час.

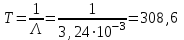
Плотность вероятности времени безотказной работы

1/час.

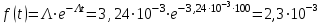
Пример 6.6. Система состоит из трех элементов с равной вероятностью безотказной работы равной 0,9. Определить вероятности безотказной работы системы при различных вариантах резервирования.

Решение: а) расчет показателей надежности системы без резервирования:

Вероятность безотказной работы системы без резервирования определяется по формуле (2.1):

,

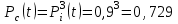
Вероятность отказа системы без резервирования определяем по формуле (2.5)

.

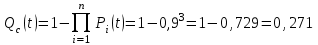
б) расчет показателей надежности системы при общем резервировании:

Структурная схема системы с общим резервированием показана на рисунке 3.3.

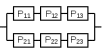
Рисунок 6.1 – Схема системы с общим резервирование:

Р₁₁, Р₁₂, Р₁₃ – вероятности безотказной работы элементов основной системы;

Р₂₁, Р₂₂, Р₂₃ – вероятности безотказной работы элементов резервной системы

Вероятность отказа системы с общим резервированием определяется по формуле (2.6):

,

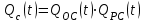
где Q_OC(t) – вероятность отказа основной системы;

Q_PC(t) – вероятность отказа резервной системы.

Вероятность отказа основной системы определяем по формуле (2.5)

.

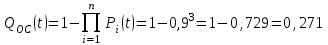
Вероятность отказа резервной системы равна

.

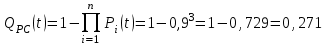
Вероятность отказа системы:

.

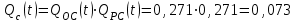
Вероятность безотказной системы с общим резервированием определяем по формуле (2.8)

.

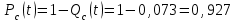
в) расчет показателей надежности системы при поэлементном резервировании:

Структурная схема системы с поэлементным резервированием показана на рисунке 3.4.

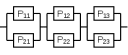
Рисунок 6.2 – Схема системы с поэлементным резервирование:

Р₁₁, Р₁₂, Р₁₃ – вероятности безотказной работы основных элементов;

Р₂₁, Р₂₂, Р₂₃ – вероятности безотказной работы резервных элементов

Вероятность безотказной работы системы с поэлементным резервированием определяем по формуле (2.6):

,

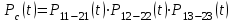
где Р_11-21(t) – вероятность безотказной работы группы из первого основного и резервного элементов;

Р_12-22(t) – вероятность безотказной работы группы из второго основного и резервного элементов;

Р_13-23(t) – вероятность безотказной работы группы из третьего основного и резервного элементов.

Вероятность безотказной работы системы с поэлементным резервированием:

,

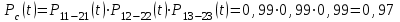
Так как вероятности безотказной работы групп элементов близки к единице, можно было воспользоваться формулой для приближенного расчета (2.3):

.

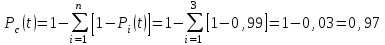
Вероятность отказа основной системы определяем по формуле (2.5)

.

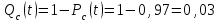
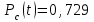
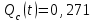
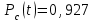
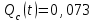
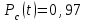
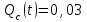
Ответ: для системы без резервирования: , ; для системы с общим резервированием , ; для системы с поэлементным резервированием: , . Таким образом, максимальная надежность достигается при поэлементном резервировании.

Задания для самостоятельной работы студентов

Задача 7.1. Определить вероятность безотказной работы системы, состоящей из 500 элементов, если вероятность безотказной работы каждого элемента в течение времени tравна P(t) = 0,998.

Задача 7.2. Вероятность безотказной работы системы, состоящей из 150 равнонадежных элементов, в течение времени t равна Р_c(t)=0,95. Найти вероятность безотказной работы элемента.

Задача 7.3. Блок управления состоит из 5000 элементов, средняя интенсивность отказов которых равна 2,3·10^-6 1/час. Определить вероятность безотказной работы в течении t = 100 час и среднее время безотказной работы.

Задача 7.4. Система состоит из пяти элементов, среднее время безотказной работы которых равно: Т₁=104 час; Т₂=200 час; Т₃=185 час; Т₄=350 час; Т₅=620 час. Показатели распределены по экспоненциальному закону. Определить среднее время безотказной работы системы.

Задача 7.5. Прибор состоит из пяти блоков. Вероятность безотказной работы каждого блока в течение времени t = 50 час равна: P₁(50)=0,98; P₂(50)=0,99; P₃(50)=0,998; P₄(50)=0,975; P₅(50)=0,985. Справедлив экспоненциальный закон надежности. Требуется найти среднее время безотказной работы прибора.

Задача 7.6. Установка состоит из 3000 элементов, средняя интенсивность отказов которых 3,8·10^-6 1/час. Определить вероятность отказа установки в течении t = 300 час и среднее время безотказной работы аппаратуры.

Задача 7.7. Объект состоит из 200000 элементов, средняя интенсивность отказов которых 0,2·10^-6 1/час. Определить вероятность безотказной работы системы в течение 240 часов и среднее время безотказной работы.

Задача 7.8. Прибор состоит из 5 узлов. Надежность узлов характеризуется вероятностью безотказной работы в течение времени t , которая равна: P₁(t)=0,98; P₂(t)=0,99; P₃(t)=0,998; P₄(t)=0,975; P₅(t)=0,985. Необходимо определить вероятность безотказной работы прибора.

Задача 7.9. Определить количество равнонадежных резервных элементов с вероятностью безотказной работы P_i(t)=0,9,необходимых для того, чтобы обеспечить вероятность безотказной работы системы равную P_с(t)=0,99.

Задача 7.10. Система состоит из четырех элементов, имеющих интенсивность отказов равную λ₁ = 2,7·10^-7 1/час, λ₂ = 3,2·10^-7 1/час, λ₃ = 2,1·10^-7 1/час, λ₄ = 4,3·10^-7 1/час. Изобразить структурную схему системы и определить вероятность безотказной работы и вероятность отказа в течение 60 часов при общем резервировании системы.

Задача 7.11. Система состоит из четырех элементов, имеющих интенсивность отказов равную λ₁ = 2,7·10^-7 1/час, λ₂ = 3,2·10^-7 1/час, λ₃ = 2,1·10^-7 1/час, λ₄ = 4,3·10^-7 1/час. Изобразить структурную схему системы и определить вероятность безотказной работы и вероятность отказа в течение 60 часов при

Задача 7.16 Система состоит из трех элементов с вероятностью безотказной работы равной P₁(t)=0,9, P₂(t)=0,92, P₃(t)=0,87. Определить время безотказной работы системы при поэлементном резервировании.

Контрольные вопросы:

1. Дайте характеристику сложной системы.
2. Как рассчитываются показатели надежности системы без резервирования (основной системы)?
3. Что такое резервирование?
4. Какие используются виды резервирования?
5. Дайте определение и характеристику общему и поэлементному резервированию.
6. Дайте определение и характеристику постоянному резервированию и резервированию замещением.
7. Дайте определение и характеристику резервированию с восстановлением и без восстановления.

Вероятность отказа основной системы определяем по формуле (2.5)

Вероятностью безотказной работы аппаратуры называется вероятность того, что она будет сохранять свои характеристики (параметры) в заданных пределах в течение определенного промежутка времени при определенных условиях эксплуатации, или, короче, – вероятностью безотказной работы аппаратуры называется вероятность того, что в определенных условиях эксплуатации в пределах заданной продолжительности работы отказ не возникает.

В дальнейшем эта характеристика обозначается P(t).

Пусть t – время, в течение которого необходимо определить вероятность безотказной работы, а Т_{1 –} время работы аппаратуры от ее включения до первого отказа. Тогда, согласно определению вероятности безотказной работы, справедливо выражение:

,                                                     (1.1)

т.е. вероятность безотказной работы – это вероятность того, что время Т₁ от момента включения аппаратуры до ее отказа будет больше или равно времени t, в течение которого определяется вероятность безотказной работы.

Из определения вероятности безотказной работы видно, что эта характеристика является функцией времени. Она имеет следующие очевидные свойства:

1) P(t) является убывающей функцией времени;

2) ;

3) Р(0) = 1,      .

На практике для определения P(t) из статистических данных об отказах аппаратуры обычно используются методы непосредственного подсчета вероятностей. Вероятность безотказной работы определяется следующей статистической оценкой:

,                                            (1.2)

где N₀ – число образцов аппаратуры в начале испытания, n(t) – число отказавших образцов за время t.

При увеличении числа образцов N₀ статистическая оценка вероятности обнаруживает устойчивость, т.е. слабо отличается от вероятности безотказной работы:

.                                  (1.3)

На практике иногда более удобной характеристикой является вероятность неисправной работы, или вероятность отказов. Эта характеристика может быть полезна, например, при сравнение надежности резервированной и не резервированной систем. Исправная работа и отказ являются событиями несовместными и противоположными. Поэтому вероятность безотказной работы и вероятность отказа Q(t) связаны зависимостью:

Q (t) = 1 – P (t),                                         (1.4)

или с учетом выражения (1.1)

Q (t) = P (T₁  t)                                         (1.5)

Из выражения (1.5) видно, что вероятность отказа является интегральной функцией распределения времени работы (Т₁) до отказа, т.е.

Q (t) = F (t)                                            (1.6)

Производная от интегральной функции распределения есть дифференциальный закон (плотность) распределения:

.                                                  1.7)

Тогда на основании выражений (1.6) и (1.7) получим:

,                                                (1.8)

т.е.

производная от вероятности отказа подчиняется дифференциальному закону распределения времени работы (Т₁) аппаратуры до ее отказа.

Для статистического определения вероятности отказа воспользуемся выражениями (1.4)и (1.3). Подставляя в выражение (1.4) вместо P(t) его выражение из формулы (1.3), получим:

.                                                       (1.9)

Вероятность безотказной работы P(t), как количественная характеристика надежности, обладает следующими достоинствами:

1) характеризует изменение надежности во времени;

2) входит во многие другие характеристики аппаратуры, а поэтому может быть полезна широкому кругу лиц, занимающихся вопросами проектирования, эксплуатации, ремонта и т.п. Например, вероятность безотказной работы наряду с точностью и живучестью определяет боевую эффективность оружия, а поэтому является необходимой для исследователя военных операций и полководца. Она определяет также стоимость изготовления и эксплуатации аппаратуры, а поэтому может быть полезной инженеру-экономисту;

3) охватывает большинство факторов, существенно влияющих на надежность аппаратуры, и поэтому достаточно полно характеризует надежность;

4) может быть сравнительно просто получена расчетным путем до изготовления системы. Это позволяет выбрать оптимальную в смысле надежности структуру системы и ее принципиальную схему;

5) является удобной характеристикой надежности, как простейших элементов, так и сложных систем и даже комплексов.

Указанные достоинства вероятности безотказной работы явились причиной наибольшего распространения этой характеристики.

Однако вероятность безотказной работы имеет также существенные недостатки:

1) характеризует надежность восстанавливаемых систем только до первого отказа, а поэтому является достаточно полной характеристикой надежности только систем разового использования;

2) не позволяет охарактеризовать зависимость между временными составляющими цикла эксплуатации; это не дает возможности установить, даже в вероятностном смысле, будет ли система готова к действию в данный момент времени или нет;

3) не всегда удобна для оценки надежности простых элементов, в особенности таких, у которых отсутствует старение;

4) по известной вероятности безотказной работы бывает трудно вычислить другие количественные характеристики надежности.

Эти недостатки позволяют сделать вывод, что вероятность безотказной работы, как, впрочем, и любая другая характеристика, не полностью характеризует такое свойство как надежность, и поэтому не может быть с ним отождествлена.