Закажите у меня новую работу, просто написав мне в чат!
Время безотказной работы электронной лампы по 16 наблюдениям составило 51; 49; 50,5; 52; 49,5; 50; 52; 51; 50; 51; 49; 50; 53; 53; 49; 50 часов. Построить 90% доверительный интервал для математического ожидания и дисперсии времени безотказной работы.
Составим сгруппированный ряд распределения банков по числу ламп. (𝑥𝑖 − время безотказной работы, 𝑛𝑖 − число ламп). Общее число значений Определим для данной выборки выборочное среднее 𝑎 и среднее квадратическое отклонение Исправленная выборочная дисперсия равна 𝑆Найдем доверительные интервалы для математического ожидания 𝑎 при доверительной вероятности 𝛾 = 0,9. Тогда по таблице значений 𝑡𝛾,𝑛 находим:

|
Tn |
|||||||||||||||||
|
n |
|||||||||||||||||
|
P |
U |
Ф(U )-Ф(-U )=2Ф(U |
)-1= , |
||||||||||||||
|
Tn |
|||||||||||||||||
|
1 |
|||||||||||||||||
|
здесь U = 1 |
|||||||||||||||||
|
2 |
|||||||||||||||||
|
Переписав это соотношение в виде: |
|||||||||||||||||
|
U |
Tn |
U Tn |
|||||||||||||||
|
P T |
T |
, |
|||||||||||||||
|
n |
n |
n |
n |
||||||||||||||
|
U |
Tn |
|||||||
|
получаем, что |
T |
– асимптотический — |
||||||
|
n |
n |
|||||||
доверительный интервал для θ. Асимптотическая дисперсия
2 ( ) n характеризует разброс распределения статистики Тn
около θ.
Интервал тем уже, чем выше асимптотическая эффективность оценки (чем меньше ()). Асимптотически кратчайший доверительный интервал будет порождаться асимптотически эффективной оценкой. Если исходная модель F регулярна, то перечисленными свойствами обладают оценки максимального правдоподобия. Таким образом, асимптотически кратчайшим — доверительным интервалом
для θ с учѐтом того, что L 
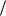
|
* |
U |
, * |
U |
1 |
1 |
||||||||||||
|
* |
, U |
. |
|||||||||||||||
|
* |
|||||||||||||||||
|
m |
ni( m ) |
m |
ni( m ) |
2 |
Если распределение генеральной совокупности не является нормальным, то в отдельных случаях по выборкам большого объѐма можно построить доверительные интервалы для неизвестных параметров приближѐнно, используя предельные теоремы теории вероятностей и вытекающие из них асимптотические распределения и оценки.
141

Пример 1. (доверительные интервалы для вероятности успеха в схеме Бернулли). Пусть в n независимых испытаниях успех наступил х раз. Найти доверительный интервал для вероятности р успеха в одном испытании.
Решение: Эффективной оценкой вероятности успеха р в
|
~ |
h |
x |
n . |
|
одном испытании является относительная частота p |
По теореме Муавра-Лапласа относительная частота h имеет
|
асимптотически нормальное распределение N(p, |
pq n ), где |
||||||
|
q=1-p. |
|||||||
|
Рассмотрим |
статистику U= (h p) |
, которая, |
|||||
|
pq n |
|||||||
|
следовательно, |
имеет |
асимптотически |
нормальное |
распределение N(0,1) независимо от значения р. При n имеем:
|
h p |
||||||||
|
P |
U |
1 |
||||||
|
pq n |
||||||||
|
2 |
||||||||
Отсюда получаем, что с вероятностью выполняется неравенство
|
h U1 |
pq |
p h U1 |
pq |
(5.17) |
||||||
|
n |
n |
|||||||||
|
2 |
2 |
|||||||||
Заменяя значения р и q в левых и правых частях неравенства
|
(5.17) их оценками |
~ |
h |
и |
~ |
1 h , получаем, что |
|
p |
q |
доверительный интервал для вероятности успеха в схеме Бернулли приближѐнно имеет вид
|
h U1 |
h(1 h) |
p h U1 |
h(1 h) |
. |
(5.18) |
|||||
|
n |
n |
|||||||||
|
2 |
2 |
|||||||||
Пример 2. При проверке 100 деталей из большой партии обнаружено 10 бракованных деталей.
а) Найти 95% приближѐнный доверительный интервал доли бракованных деталей во всей партии.
142
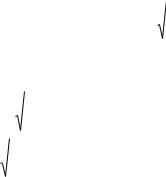
б) Какой минимальный объѐм выборки следует взять для того, чтобы с вероятностью 0.95 утверждать, что доля бракованных деталей во всей партии отличается от частоты появления бракованных деталей в выборке не более, чем на 1% .
Решение:
а) Оценка доли бракованных деталей в партии по выборки
равна ~ =10/100=0.1. По таблице квантилей нормального p h
распределения [12] находим квантиль U0.975=1.96. По формуле (5.18) 95-% интервал приближѐнно имеет вид 0.041<p<0.159. б) Представим доверительный интервал (5.18) в виде
|
неравенства |
h p |
U1 |
h(1 h) |
, которое выполняется с |
||||
|
n |
||||||||
|
2 |
||||||||
|
вероятностью =0.95. Так как по условию задачи |
x-p 0.01, |
||||||||||||
|
то |
для |
определения |
n |
получим |
неравенство |
||||||||
|
U0.975 |
h(1 h) |
0.01, |
отсюда |
следует, |
что |
||||||||
|
n |
|||||||||||||
|
196. |
01. (1 01.) |
0.01 и |
n (0.3 196)2=3457.44. |
Значит, |
|||||||||
|
n |
минимальный объем выборки n=3458
Задачи и решения
Интервальное оценивание. Доверительные интервалы
Врассматриваемых задачах предполагается, что выборка объема n получена из генеральной совокупности, имеющей либо нормальное распределение, либо распределение, достаточно близкое к нормальному.
Взадачах 40, 41 выборочные оценки определились по результатам n наблюдений. Используя формулы, приведенные
втаблице, найти 90%- и 99%-ные доверительные интервалы для математического ожидания (среднего) следующих характеристик:
143

Задача 40
Емкость конденсатора, если x =20 мкФ, n=16, среднеквадратичное отклонение известно и равно 4мкФ
Решение:
|
x 20, n 16, * |
u; |
||||||||||||||||||||||||||||||
|
P |
1 0, 9 |
0, 95 |
|||||||||||||||||||||||||||||
|
1 |
2 |
||||||||||||||||||||||||||||||
|
P |
1 0, 99 |
0, 995 |
|||||||||||||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||||||||||||
|
x0,5 |
1, 645 |
||||||||||||||||||||||||||||||
|
j |
|||||||||||||||||||||||||||||||
|
x0,995 2, 576 |
|||||||||||||||||||||||||||||||
|
x |
x0,95 |
M x |
x0,95 |
||||||||||||||||||||||||||||
|
n |
n |
||||||||||||||||||||||||||||||
|
20 |
1, 645 |
u |
M 20 |
1, 645 |
u |
M 18, 35; 21, 64 |
|||||||||||||||||||||||||
|
16 |
16 |
||||||||||||||||||||||||||||||
|
20 |
2, 576 |
u |
M 20 |
2, 576 |
u |
M 17, 424; 22, 576 |
|||||||||||||||||||||||||
|
16 |
16 |
Ответ : 18, 35; 21, 64 , 17, 424; 22, 576 ;
Задача 41
Время безотказной работы электронной лампы, если
x =500, n=100 среднеквадратичное отклонение известно и равно10 часов.
Решение:
144

|
x 500, n 100, 10 |
|||||||||||||||||||||
|
1) |
500 |
1, 645*10 |
M 500 |
1, 645*10 |
|||||||||||||||||
|
10 |
10 |
||||||||||||||||||||
|
498,355<M<501,645 |
|||||||||||||||||||||
|
2) |
500 |
2,576*10 |
M 500 |
2,576*10 |
|||||||||||||||||
|
10 |
10 |
||||||||||||||||||||
|
497,424<M<502,576 |
|||||||||||||||||||||
|
Ответ: 498,355;501,645 , 497,424;502,576 ; |
|||||||||||||||||||||
|
Пусть из одной генеральной совокупности получены две |
|||||||||||||||||||||
|
выборки |
объемов |
n1 и |
n2 соответственно. |
Выборочные |
|||||||||||||||||
|
оценки |
средних |
и дисперсий |
по этим |
выборкам равны |
|||||||||||||||||
|
x , x ; S2 |
, S2 . Объединенные оценки среднего и дисперсии по |
||||||||||||||||||||
|
1 |
2 |
2 |
|||||||||||||||||||
|
выборке объема n1 n2 вычисляются по формулам |
|||||||||||||||||||||
|
x |
n x n x |
, S 2 |
n 1 S 2 n 1 S 2 |
||||||||||||||||||
|
1 1 |
2 2 |
1 |
1 |
2 |
2 |
. |
|||||||||||||||
|
n1 n2 |
n1 n2 2 |
||||||||||||||||||||
Показать, что если дисперсия генеральной совокупности
известна и равна 2 , то доверительный интервал для среднего определяется так:
|
x |
S |
t |
n n 2 m x |
S |
t |
n n 2 |
||||||
|
.(*) |
||||||||||||
|
n |
n |
1 |
1 2 |
n n |
1 |
1 2 |
||||||
|
1 |
2 |
2 |
1 |
2 |
2 |
Для уточнения характеристик, приведенных в задачах 40, 41 были проделаны повторные эксперименты и получены новые выборочные оценки. Найти 90%- и 99%-ные доверительные интервалы для среднего, используя формулу (*).
145
|
Задача 42 |
||||||||||||||
|
Емкость конденсатора, если n=16, |
x =18 мкФ. |
|||||||||||||
|
Решение: |
||||||||||||||
|
x1 20 |
n1 16 |
|||||||||||||
|
x2 18 |
n2 |
19 |
=4 |
|||||||||||
|
x |
n1 x1 |
n2 x2 |
20 16 9 18 |
19, 28 |
||||||||||
|
n1 n2 |
||||||||||||||
|
25 |
||||||||||||||
|
19, 28 |
4 1, 645 |
M 19, 28 |
4 1, 645 |
|||||||||||
|
5 |
5 |
|||||||||||||
|
M 17,964; 20,596 |
||||||||||||||
|
19, 28 |
4 2,576 |
M 19, 28 |
4 2,576 |
|||||||||||
|
5 |
5 |
|||||||||||||
|
M 17, 2192; 21,3408 |
||||||||||||||
|
Ответ : M 17,964; 20,596 ; |
M 17, 22; 21,34 |
Задача 43
Время безотказной работы электронной лампы, если
n=64, x =480 ч.
Решение:
146

|
x1 500 |
x2 |
480 |
|||||||||||||||||||||||||
|
n1 100 |
n2 |
64 |
=10 |
||||||||||||||||||||||||
|
x |
n1 x1 n2 x2 |
500 100 480 64 |
492,19 |
||||||||||||||||||||||||
|
n1 n2 |
164 |
||||||||||||||||||||||||||
|
492,19 10 |
1, |
645 |
M 492,19 10 |
1, |
645 |
||||||||||||||||||||||
|
164 |
164 |
||||||||||||||||||||||||||
|
492,19 1, 285 M 492,19 1, 285 |
|||||||||||||||||||||||||||
|
M 490,905; 493, 478 |
|||||||||||||||||||||||||||
|
492,19 |
10 2,576 |
M 492,19 |
10 2,576 |
||||||||||||||||||||||||
|
12,8 |
12,8 |
||||||||||||||||||||||||||
|
M 490,177; 494, 2025 |
|||||||||||||||||||||||||||
|
Ответ : M 490,905; 493, 478 ; |
M 490,177; 494, 2025 |
||||||||||||||||||||||||||
|
Задача 44 |
|||||||||||||||||||||||||||
|
Диаметр вала, если n1=9, x =30 мм, |
S 2 =9 мм2 , n2=16, |
||||||||||||||||||||||||||
|
x =29 мм, S 2 =4,5 |
мм2 . |
||||||||||||||||||||||||||
|
Решение: |
|||||||||||||||||||||||||||
|
n 9; n |
16; |
x |
30; x |
29; S |
2 9; |
S 2 |
4,5. |
||||||||||||||||||||
|
1 |
2 |
1 |
2 |
1 |
2 |
||||||||||||||||||||||
|
x |
S |
t1 |
n1 n2 m x |
S |
t1 n1 n2 |
||||||||||||||||||||||
|
n1 n2 |
|||||||||||||||||||||||||||
|
n1 n2 |
2 |
2 |
|||||||||||||||||||||||||
|
1) |
1- 0,90; |
t 1, 714; |
|||||||||||||||||||||||||
|
2 |
1 |
2 |
|||||||||||||||||||||||||
|
2) |
1- 0,99; |
t |
1,807; |
||||||||||||||||||||||||
|
2 |
1 |
2 |
|||||||||||||||||||||||||
|
x |
n1 x1 n2 x2 |
9,30 16, 29 |
29,36 |
||||||||||||||||||||||||
|
n1 n2 |
25 |
||||||||||||||||||||||||||
|
S 2 n1 1 S12 |
n2 |
1 S22 |
8 9 15 4,5 |
6, 06 |
|||||||||||||||||||||||
|
n1 n2 2 |
23 |
||||||||||||||||||||||||||
|
28,51 m 30, 20 |
27,98 m 30, 74
Ответ : 28,51;30, 20 ; 27,98;30, 74
147
Задача 45
По данным задачи 44 найти 90%- и 95%-ный доверительные интервалы для дисперсии.
Решение:
|
n 16; |
x 29; S 2 |
45; |
(0,9;0,95); |
||||||||||||||||||
|
nS 2 |
2 |
nS 2 |
|||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||
|
1 |
n |
1 |
n |
||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||
|
1 |
0, 05; |
1 |
0,95; |
1 |
0, 025; |
1 |
0,975; |
||||||||||||||
|
2 |
2 |
2 |
2 |
||||||||||||||||||
|
16 4,5 |
2 |
16 4,5 |
2 2, 74;9, 04 |
||||||||||||||||||
|
26, 2 |
7,962 |
||||||||||||||||||||
|
0,952 |
16 7,962 |
0,052 |
16 26, 2; |
||||||||||||||||||
|
0,9752 |
16 6, 67 |
0,0252 |
16 29,3; |
||||||||||||||||||
|
16 4,5 |
2 |
16 4,5 |
2 |
2, 457;10, 79 |
|||||||||||||||||
|
29,3 |
6, 67 |
||||||||||||||||||||
|
Ответ : 2, 7;9, 04 ; |
2, 45;10, 79 ; |
Задача 46
С автоматической линии, производящей подшипники, было отобрано 400 штук, причем 10 оказалось бракованными. Найти 90%-ный доверительный интервал для вероятности появления бракованного подшипника. Сколько подшипников надо проверить, чтобы с вероятностью 0,9973 можно было утверждать, что вероятность появления бракованного подшипника не отличается от частоты более чем на 5%?
Решение:
148
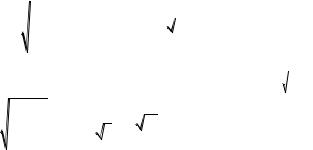
|
n 400; |
0,9; |
u Ф 1 |
(0,9) 1, 67; |
|||||||||||||||||||||||||||||
|
pˆ |
10 |
1 |
||||||||||||||||||||||||||||||
|
400 |
40 |
|||||||||||||||||||||||||||||||
|
1 |
39 |
|||||||||||||||||||||||||||||||
|
1 |
1 |
39 |
||||||||||||||||||||||||||||||
|
1, 67 |
40 |
40 |
p |
1, 67 |
||||||||||||||||||||||||||||
|
40 20 |
||||||||||||||||||||||||||||||||
|
40 |
400 |
40 |
||||||||||||||||||||||||||||||
|
p 0, 012;0, 038 |
т.к p2 |
p 0, 05; |
pˆ p u |
|||||||||||||||||||||||||||||
|
ˆ ˆ |
||||||||||||||||||||||||||||||||
|
1 |
p 1 p |
|||||||||||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||||||
|
1 |
39 |
|||||||||||||||||||||||||||||||
|
3 39 |
||||||||||||||||||||||||||||||||
|
3 10 |
10 |
0, 05 |
9,367 |
|||||||||||||||||||||||||||||
|
n3 |
||||||||||||||||||||||||||||||||
|
n |
40 0, 05 |
|||||||||||||||||||||||||||||||
|
n 87, 75 |
||||||||||||||||||||||||||||||||
|
Ответ : |
0,012;0,038 |
n 88; |
Лабораторная работа № 5
Целью лабораторной работы является изучение интервального оценивания параметров нормального распределения в пакете MATHCAD.
Точечные оценки дают приближенное значение неизвестного (оцениваемого) параметра. Сама оценка является случайной величиной, и если известно ее распределение или хотя бы дисперсия, то можно указать пределы, в которых с достаточно большой вероятностью лежит неизвестное значение параметра. Эти пределы легко вычисляются через дисперсию. Важно понимать, что пользоваться полученными значениями пределов можно, только если они не зависят от самого оцениваемого параметра.
ЗАДАНИЕ
Найдите доверительные интервалы для математического ожидания MX и дисперсии DX по заданной выборке x1,x2,…,xn из нормального распределения.
Порядок выполнения задания
1. Определите и введите компоненты вектора выборочных значений случайной величины.
149
2.Вычислите точечные оценки MX и DX.
3.Вычислите 95%-ный доверительный интервал для математического ожидания при неизвестной дисперсии.
4.Вычислите 90%-ный доверительный интервал для дисперсии.
Пример выполнения задания
Найдите доверительные интервалы для математического ожидания и дисперсии приведенной выборки из нормального распределения.
|
x |
904.3 |
910.2 |
916.6 |
928.8 |
935.0 |
941.2 |
|
n |
3 |
1 |
2 |
7 |
8 |
10 |
|
x |
947.4 |
953.6 |
959.8 |
966.0 |
972.2 |
978.4 |
|
n |
4 |
2 |
4 |
1 |
1 |
1 |
Фрагмент рабочего документ MATHCAD с вычислениями доверительных интервалов представлен ниже (в приведенном фрагменте опущено определение массива DX, который во втором столбце содержит значения случайной величины, а в первом – их количество в выборке).
|
ORIGIN :=1 |
i:=1 12 |
||||||
|
12 |
|||||||
|
n : Di ,1 |
n = 44 |
||||||
|
i 1 |
|||||||
|
1 |
12 |
||||||
|
Mx : |
Di ,1Di , 2 |
Mx = 938.693 |
|||||
|
n i 1 |
|||||||
|
1 |
12 |
||||||
|
Dx : |
Di ,1 (Di , 2 |
Mx)2 Dx = 282.988 |
|||||
|
n |
1 |
||||||
|
i 1 |
|||||||
95%-ный доверительный интервал для математического ожидания
150
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
1. Доверительный интервал. Доверительная вероятность.
Семинар 21
2.
Доверительным интервалом для параметра называется интервал
( 1, 2), содержащий истинное значение параметра с заданной
вероятностью p=1- .
p — доверительная вероятность,
— уровень значимости.
3.
Доверительные интервалы для параметров m и 2
нормально распределенной генеральной совокупности
Параметр
Предположения
m
2 известно
m
2
2
2 неизвестн
о 2
2
~
S
mизвестно
mнеизвестн
о
Оценка
Распределение
параметра
оценки
n
1
X xi
n i 1
n
1
X xi
n i 1
S 02
X N m,
n
2
2
2 (n)
S02
1 n
( xi m) 2
n i 1
S
2
(n 1)
(n 1)
2
1 n
2
S
( xi X )
n 1 i 1
u1 / 2 m
n
n
u1 / 2
S
t1 / 2 (n 1) m
n
S
X
t1 / 2 (n 1)
n
X
S02
n
X
X m
T (n 1)
S/ n
2
S2
X
1 n
2
S
( xi X )
n 1 i 1
Доверительный интервал
2
nS02
nS02
2
2
2
1 / 2 (n)
/ 2 ( n )
( n 1) S 2
2
2
1 / 2 ( n 1)
( n 1) S 2
2 / 2 ( n 1)
4. Квантили u нормального распределения
Квантили u нормального распределения
P
0.90
0.95
0.975
0.99
0.995
0.999
0.9995
up
1.282
1.645
1.960
2.236
2.576
3.090
3.291
5.
Квантили распределения Стьюдента
0,75
0,9
0,95
0,975
0,99
0,995
0,999
1
1,000
3,078
6,314
12,706
31,821
63,657
318,309
2
0,816
1,886
2,920
4,303
6,965
9,925
22,327
3
0,765
1,638
2,353
3,182
4,541
5,841
10,215
4
0,741
,533
2,132
2,776
3,747
4,604
7,173
5
0,727
,476
2,015
2,571
3,365
4,032
5,893
6
0,718
,440
1,943
2,447
3,143
3,707
5,208
7
0,711
,415
1,895
2,365
2,998
3,499
4,785
8
0,706
,397
1,860
2,306
2,896
3,355
4,501
9
0,703
,383
1,833
2,262
2,821
3,250
4,297
10
0,700
,372
1,812
2,228
2,764
3,169
4,144
11
0,697
,363
1,796
2,201
2,718
3,106
4,025
12
0,695
,356
1,782
2,179
2,681
3,055
3,930
13
0,694
,350
1,771
2,160
2,650
3,012
3,852
14
0,692
,345
1,761
2,145
2,624
2,977
3,787
15
0,691
,341
1,753
2,131
2,602
2,947
3,733
16
0,690
,337
1,746
2,120
2,583
2,921
3,686
17
0,689
,333
1,740
2,110
2,567
2,898
3,646
6.
Квантили распределения Стьюдента (продолжение)
0,75
0,9
0,95
0,975
0,99
0,995
0,999
18
0,688
,330
1,734
2,101
2,552
2,878
3,610
19
0,688
,328
1,729
2,093
2,539
2,861
3,579
20
0,687
,325
1,725
2,086
2,528
2,845
3,552
21
0,686
,323
1,721
2,080
2,518
2,831
3,527
22
0,686
,321
1,717
2,074
2,508
2,819
3,505
23
0,685
,319
1,714
2,069
2,500
2,807
3,485
24
0,685
,318
1,711
2,064
2,492
2,797
3,467
25
0,684
,316
1,708
2,060
2,485
2,787
3,450
26
0,684
1,315
1,706
2,056
2,479
2,779
3,435
27
0,684
1,314
1,703
2,052
2,473
2,771
3,421
28
0,683
1,313
1,701
2,048
2,467
2,763
3,408
29
0,683
1,311
1,699
2,045
2,462
2,756
3,396
30
0,683
1,310
1,697
2,042
2,457
2,750
3,385
40
0,681
1,303
1,684
2,021
2,423
2,704
3,307
60
0,679
1,296
1,671
2,000
2,390
2,660
3,232
120
0,677
1,289
1,658
1,980
2,358
2,617
3,160
200
0,676
1,286
1,653
1,972
2,345
2,601
3,131
7.
Квантили хи-квадрат распределения
χ 2p(k)
0,005
0,01
0,025
0,05
0,1
0,2
0,3
0,7
0,8
0,9
0,95
0,975
0,99
0,995
0,999
1
3,9Е-05
0,0002
0,001
0,004
0,02
0,1
0,1
1,1
1,6
2,7
3,8
5,0
6,6
7,9
10,8
2
0,010
0,02
0,051
0,10
0,21
0,45
0,71
2,41
3,22
4,61
5,99
7,38
9,21
10,60
13,82
3
0,072
0,11
0,22
0,35
0,58
1,01
1,42
3,66
4,64
6,25
7,81
9,35
11,34
12,84
16,27
4
0,21
0,30
0,48
0,71
1,06
1,65
2,19
4,88
5,99
7,78
9,49
11,14
13,28
14,86
18,47
5
0,41
0,55
0,83
1,15
1,61
2,34
3,00
6,06
7,29
9,24
11,07
12,83
15,09
16,75
20,52
6
0,68
0,87
1,24
1,64
2,20
3,07
3,83
7,23
8,56
10,64
12,59
14,45
16,81
18,55
22,46
7
0,99
1,24
1,69
2,17
2,83
3,82
4,67
8,38
9,80
12,02
14,07
16,01
18,48
20,28
24,32
8
1,34
1,65
2,18
2,73
3,49
4,59
5,53
9,52
11,03
13,36
15,51
17,53
20,09
21,95
26,12
9
1,73
2,09
2,70
3,33
4,17
5,38
6,39
10,66
12,24
14,68
16,92
19,02
21,67
23,59
27,88
10
2,16
2,56
3,25
3,94
4,87
6,18
7,27
11,78
13,44
15,99
18,31
20,48
23,21
25,19
29,59
11
2,60
3,05
3,82
4,57
5,58
6,99
8,15
12,90
14,63
17,28
19,68
21,92
24,72
26,76
31,26
12
3,07
3,57
4,40
5,23
6,30
7,81
9,03
14,01
15,81
18,55
21,03
23,34
26,22
28,30
32,91
13
3,57
4,11
5,01
5,89
7,04
8,63
9,93
15,12
16,98
19,81
22,36
24,74
27,69
29,82
34,53
14
4,07
4,66
5,63
6,57
7,79
9,47
10.82
16,22
18,15
21,06
23,68
26,12
29,14
31,32
36,12
15
4,60
5,23
6,26
7,26
8,55
10,31
11,72
17,32
19,31
22,31
25,00
27,49
30,58
32,80
37,70
16
5,14
5,81
6,91
7,96
9,31
11,15
12,62
18,42
20,47
23,54
26,30
28,85
32,00
34,27
39,25
8.
Задача 3.2.
Найти 90% и 99% доверительные интервалы для времени безотказной
работы электронной лампы, если X 500 часов, n=100, с.к.о. известно и
равно 10 часов.
Решение.
X m
N ( 0,1)
/ n
Рассмотрим статистику
1) 90%
=0,1; /2=0.05; 1- /2= 0.95
u1 / 2 1.645
10
10
500
1.645 m 500
1.645
100
100
498.355< m < 501.645
2) 99%; =0,01; /2=0.005; 1- /2= 0.995
u1 / 2 2.576
500
497.42<m<502.56
10
10
2.576 m 500
2.576
100
100
9.
Задача 3.3.
Найти 90% доверительный интервал для диаметра вала, если n=9,
X 30 мм , оценка для дисперсии равна 9 мм2.
Решение.
90%
=0,1
t1 / 2 (9 1) t0.950 (8) 1.860
30
3
3
1860
.
m 30
1860
.
9
9
28.14<m<31.86
10.
Задача 3.12.
Результаты 10 измерений емкости конденсатора прибором, не имеющим
систематической ошибки, дали такие отклонения от номинала:
5,4
-13,9
-11
7,2
-15,6
29,2
1,4
-0,3
6,6
-9,9
Найти 95% доверительный интервал для мат. ожидания и дисперсии.
Решение.
Проведем предварительные расчеты.
Сумма
( xi X )2
Среднее
5,4
-13,9
-11
7,2
-15,6
29,2
1,4
-0,3
6,6
-9,9
-0,9
30,14
191
119
53,1
240,6
858
2,22
0,04
44,8
96,2
1634,749
-0,09
1 n
X xi
n i 1
Оценка дисперсии
1 n
2
S
( xi X )
n 1 i 1
181,6
2
11.
Заметим, что мат. ожидание и дисперсия неизвестны. Следовательно,
будем пользоваться распределением Стьюдента с n-1 степенью свободы
для получения интервала для мат. ожидания и распределением хи-квадрат
с n-1 степенью свободы для оценки дисперсии.
t1 / 2 (10 1) t0.975 (9) 2.262
95% доверительный интервал ; =0,05
X m
T (n 1) ;
S/ n
1)
X
S
S
t1 / 2 (n 1) m X
t1 / 2 (n 1)
n
n
181.6
181.6
0.09
2.262 m 0.09
2.262
10
10
2)
S
2
2
(n 1)
(n 1)
2
(n 1) S 2
-9.73<m<9.55
(n 1) S 2
2
1 / 2 (n 1)
2/ 2 (n 1)
2
12 / 2 (9) 02.975 (9) 19.0 ; 2/ 2 (9) 02.025 (9) 2.70
9 181 .6
9 181 .6
2
19.0
2.70
86.02 σ 2 605.33
Дома :Найти 90% доверительный интервал для дисперсии и С.К.О.
12. Доверительные интервалы для параметра p биномиального распределения
Пусть x– наблюденное значение случайной величины X, имеющей
распределение B(n, p). Оценкой для p является относительная частота
h=x/n . Если n>50, а nh>5 ,и n(1-h)>5 , то распределение случайной
величины Z h p , q 1 p , аппроксимируется нормальным
pq
n
распределением N(0,1).Можно использовать следующие формулы для
границ p1 и p2 доверительного интервала
p1, 2 h
u1 / 2
h(1 h)
n
13.
Задача 3. 20.
Из большой партии транзисторов одного типа были случайным образом
отобраны и проверены 100 штук. У 36 транзисторов коэффициент
усиления оказался меньше 10. Найти 95%-ый доверительный интервал
для доли таких транзисторов во всей партии.
Решение.
Распределение –биномиальное B(n, p).
h=x/n=36/100=0.36 .
n= 100 >50, а nh=36>5 ,и n(1-h)=100(1-0.36)=64>5
Z
h p
N (0,1)
pq
n
95% доверительный интервал =0,05
p1, 2
u1- /2=u0.975=1.960
u1 / 2
1.96
h
h(1 h) 0.36
0.36 1 0.36 ;
n
100
0.266 p 0.454
14.
Домашнее задание. 3.4, 3.13
Доверительные интервалы для времени безотказной работы (доверительные интервалы для параметра экспоненциального закона)
Недостаточность точечных оценок
Доверительные интервалы для планов с простыми достаточными статистиками
Пример 1
Пример 2
Пример 3
Доверительные интервалы для планов с составными достаточными статистиками
Пример 4
Недостаточность точечных оценок
Какими бы хорошими свойствами эти оценки не обладали, например несмещенностью и эффективностью, все же в ряде случаев, представляющих большой практический интерес, оказывается недостаточным характеризовать качество и надежность изделий только с помощью оценок.
Если отказ элемента приводит к большому ущербу, то используются только очень надежные элементы. В случае показательного закона отказов это означает, что величина должна быть крайне мала.
Поскольку время Т проведения испытаний ограничено, то малость приводит к тому, что среднее число отказов, наблюдаемых при проведении испытаний, также мало.
Может оказаться, что при проведении испытаний отказы вообще не наблюдаются. В тех случаях, когда наблюдаемое число отказов отлично от нуля, но невелико, естественная мера разброса значений случайной оценки — отношение корня из дисперсии к математическому ожиданию — велика (>1), поэтому величина оценки резко меняется от испытания к испытанию и не может служить устойчивой характеристикой надежности элементов.
Эти критические замечания подводят нас к целесообразности использования для оценки параметра экспоненциального закона метода доверительных интервалов.
Двусторонним доверительным интервалом для параметра с коэффициентом доверия, не меньшим
, называется случайный интервал
, концы которого зависят только от исходов испытаний х и для любого
> 0
Верхним и нижним
односторонними интервалами называются такие случайные интервалы, для которых при любом
> 0 соответственно
При построении доверительных интервалов мы будем использовать общий метод. При этом в качестве случайных величин, распределение которых зависит от неизвестного параметра , мы будем брать значения достаточных статистик, которые получаются в результате проведения испытаний.
Заметим, поскольку оценки для параметра являются монотонными функциями от рассматриваемых ниже достаточных статистик, то доверительные интервалы, полученные исходя из оценок, с одной стороны, и достаточных статистик, с другой, — совпадают. Мы несколько изменим порядок изложения, рассмотрев сначала более простые планы [N, B, T], [N, B, r], [N, Б, r], [N, Б, T], а затем более сложные планы [N, B, (r, T)], [N, Б, (HS)], [N, Б, (r, T)].
Доверительные интервалы для планов с простыми достаточными статистиками
Для плана [N, B, T] достаточной статистикой является число d(T) наблюденных отказов.
d(T) — случайная величина, имеющая пуассоновское распределение с параметром . На плоскости
исходы опыта представляются в виде случайных точек
, где
— значение параметра пуассоновской величины, а d — число наблюденных отказов.
Для построения верхней границы доверительного интервала с коэффициентом доверия, не меньшим , мы должны для каждого значения
указать такое целое число
, что вероятность того, что достаточная статистика примет значение, не большее
, не превышает 1 —
, а вероятность принять не большее [
+1] — уже больше, чем 1 —
. Так как величина d(T) распределена по закону Пуассона, то
определяется из соотношения
(1)
где 
является монотонно убывающей функцией параметра
, мы получаем, что
— неубывающая функция от
. Так как d(
) принимает только целочисленные значения, то
является ступенчатой неубывающей функцией (рис. 1).
Рис. 1. Вид и
При этом из (1) следует, что впервые достигает уровня d при таком значении
, для которого
(2)
Определим множество как совокупность точек
> 0, d=0,1,2,…, для которых
d() >
. Из определения следует, что вероятность того, что случайная точка
, где
, а d(T) — число отказавших элементов, попадает в множество , ни при каком значении
не превышает 1 —
.
Событие эквивалентно тому, что значение
лежит левее случайной точки
, определяемой из (2). Вероятности эквивалентных событий равны поэтому
(3)
Таким образом, является верхней доверительной границей с коэффициентом доверия, не меньшим
. Так как
, то
является верхней доверительной границей для параметра
с тем же коэффициентом доверия
.
При построении двустороннего доверительного интервала для параметра пуассоновской случайной величины d(T) с коэффициентом доверия
выбираем два числа
и
> 0,
(обычно
=
) и строим множество
точек
, для которых или
(4)
Из условий (4) следует, что вероятность попадания случайной точки в множество
не превышает
. Учитывая, что функция
— монотонно убывающая из (4), получаем, что точка
тогда и только тогда, когда значение
лежит левее точки
и правее точки
, для которых
(5)
так как только при этом не выполняется хотя бы одно из неравенств (4). Итак, событие
эквивалентно событию
. Отсюда получаем
(6)
Значения определяются формулой
(7)
и исходя из (5), можно записать
(8)
Таким образом, интервал является доверительным с коэффициентом доверия, равным
. Учитывая снова, что
, получаем доверительный интервал для оцениваемого значения
,

где значения и
находятся как решения уравнений (5). Если d=0, то значение
(0-1) считается равным нулю. Рассмотрим некоторые примеры.
Пример 1. Предположим, что проводились испытания по плану [N=500, B, T=100] и при этом было зарегистрировано 5 отказов: d(T) = 5. Требуется найти верхний доверительный предел с коэффициентом доверия =0,9. Вычисляя, находим, что
для
=0,9. Отсюда
истинное значение с вероятностью 0,9 не превосходит найденного значения
. Построим теперь двусторонний доверительный предел, соответствующий значению
=0,9;
=
= 0,05 находим
. Отсюда по формуле (9) находим
При использовании плана [N, B, r] достаточной статистикой является момент tr, появления r-го отказа. Плотность вероятностей этой статистики задается формулой (11) из раздела Оценки времени безотказной работы. Заметим теперь, что плотность случайной величины имеет вид
(10)
т.е. не зависит от неизвестного значения параметра . Если задаться значением коэффициента доверия
и
значениями и такими, что

то из плотности (10) следует, что

Неравенства в (12) эквивалентны неравенствам 

Так как соотношение (13) выполнено для любого > 0 , то случайный интервал

с коэффициентом доверия
.
Соответственно для параметра доверительный интервал имеет вид:

Односторонний интервал с коэффициентом доверия получаем из (14), полагая
= 0,
= 1 —
. При этом ,
.
Пример 2. В результате испытаний в соответствии с планом [N=500, B, r=15] получено, что . Найти верхний доверительный интервал с коэффициентом доверия
=0,99. Вычисляя значения
, что
=25,446. Из формулы (14) получаем значение границы доверительного интервала для
Аналогичным способом можно построить доверительный интервал для плана [N, Б, r]. Здесь достаточной статистикой является суммарная наработка испытываемых элементов
, где
моменты отказов элементов.
Плотность этой статистики имеет вид (31) из раздела Оценки времени безотказной работы, поэтому случайная величина имеет плотность (10). Повторяя рассуждения, использованные при выводе формулы (13), получаем, что

Итак, двусторонний доверительный интервал для , соответствующий коэффициенту доверия
=
+
, будет иметь границы

где SБ(tr) — суммарная наработка элементов за время проведения испытаний.
Соответственно верхняя граница одностороннего интервала с коэффициентом доверия равна
План [N, Б, T]. В случае плана достаточными статистиками является число d(t) отказавших элементов и суммарная наработка Для высоконадежных элементов значение
, поэтому условная плотность распределения моментов отказов практически совпадает с плотностью равномерного распределения, так как она равна
.
Поэтому при фиксированном значении достаточной статистики S(T) распределение статистики d(T) практически не зависит от значения параметра , если только
.
Следовательно, в наиболее важной области малых значений параметра практически вся информация об этом параметре сосредоточена в достаточной статистике d(T). Исходя из этого, мы ограничиваемся только статистикой d(T). Можно было бы рассмотреть значения самой оценки для параметра
, равной
, однако этот путь приводит к громоздким, мало пригодным для использования формулам.
Так как каждый элемент может отказать независимо от отказов других элементов, а вероятность отказа , то распределение отказов d(T) является биномиальным
Функция является монотонной по p, поэтому неравенство
эквивалентно неравенству
Следовательно,

Так как при = 0,
для d=0,1,.., N, то из (17), полагая
= 0,
= 1 —
, получаем односторонний доверительный интервал

.

Из (17) находим, что двусторонний доверительный интервал имеет вид

где находятся из (18), а
— для значений
=
=
Односторонний интервал равен

где соответствующее значение находится для
= 1 —
.
Пример 3. Испытания проводятся по плану [N = 150, Б, T=100 час]. За время испытаний отказало 5 элементов. Требуется найти двусторонний доверительный интервал с коэффициентом доверия = 0,95.
Находим, что Таким образом, из формулы (19)
Доверительные интервалы для планов с составными достаточными статистиками
План [N, Б, (r, T)]. Моменты отказов образуют пуассоновский поток с интенсивностью . Основная специфика этого случая состоит в том, что достаточная статистика для параметра
является составной.
Если значение tr > T, то она равна значению d(T) числа моментов, отказавших за время T; если же tr < T, то достаточная статистика tr равна — моменту появления r-го отказа.
Рассмотрим точки плоскости вида (рис. 2)
Рис. 2. График точек плоскости вида и множества
Если в результате испытаний элементов, для которых , наблюдается значение tr<T, то результаты испытаний отмечаются случайной точкой
. Если же tr > T и число отказов равно d(T) = d, то исход опыта обозначается случайной точкой
.
Множество точек строится следующим образом. Задаемся двумя числами
,
> 0,
=1 — (
+
). При фиксированном значении
к верхней части множества
относим те точки
или t, для которых находится из условий
;
— целое число, не большее r — 1, если

если же , то
, где
находится из условий

Аналогичным образом к нижней части множества относим точки (
, S) , для которых
находится из условий

если же 
, где
— целое число, не большее r — 1, находится из условий

Вероятность того, что исход испытания будет отмечен случайной точкой не превышает 1 —
=
+
по построению множества
. Соответственно вероятность противоположного события
не меньше
.
Если в результате проведения испытаний наблюдалось отказов, то событие
эквивалентно событию
(25)
где и
— функции, обратные к
,
для тех значений
, при которых
или
равны T + r — d, d = 0, … , r — 1. Из уравнений (21) и (24) находим, что
и
определяются уравнениями


Но эти уравнения эквивалентны уравнениям (11). Отсюда находим, что

где .
Если же в момент r-го отказа tr<T, то событие эквивалентно событию
(29)
где ,
— функции, обратные к
,
для тех значений
, при которых значения
и
не превышают Т. Из (22) и (23) находим, что и определяются уравнениями


Эти уравнения эквивалентны уравнениям (11), в которых
Таким образом, построение доверительного интервала для оценки параметра при использовании плана [N, B, (r, T)] нужно производить так же, как при использовании планов [N, B, T], [N, B, r] в зависимости от того, имеем мы tr<T или tr > T .
План [N, Б, (r, HS0)]. План [N, Б, (r, HS0)] эквивалентен плану [N = 1, B, (r, S0)]. Поэтому двусторонний доверительный интервал имеет вид

(33)
где , d(t) — число элементов, отказавших к моменту t. Односторонний доверительный интервал получаем из формул (32), (33), полагая в них
= 0 , что соответствует значению
= 1 —
= 0.
Пример 4. Испытания проводились в соответствии с планом [N=500, Б, (r=20, HS0=20000)]. К моменту окончания испытаний, когда суммарная наработка стала равной 20 000, отказало 16 элементов.
Требуется найти верхний доверительный предел, соответствующий коэффициенту доверия = 0,99. Так как значение
, т.е. суммарная наработка элементов достигла уровня S0 заданного до начала испытаний, раньше, чем наступил отказ 20-го элемента, то верхняя доверительная граница находится по формуле (32). Можно получить, что
, откуда
План [N, Б, (r, T)]. Вполне аналогичным способом можно получить доверительные интервалы для случая плана [N, Б, (r, T)].
Здесь достаточная статистика равна либо наработке S(tr) к моменту tr, если , либо является двумерной (d(T), SБ(T)), если tr>T, где d(T) — число отказавших элементов, а
— суммарная наработка. Однако по тем же соображениям, которые приводились для случая плана [N, Б, T], статистику SБ(T) мы исключаем из рассмотрения.
Итак, значение случайной величины, исходя из которой мы строим доверительный интервал, равно d(T), если tr>T, и равно , если tr<T. На плоскости
мы рассматриваем множество точек
где — взаимно независимые неотрицательные случайные величины с плотностью, равной
. Поэтому

Соответственно (35)
Далее, в точности повторяя все рассуждения, использованные при построении множества и затем доверительных интервалов для плана [N, B, (r, T)], и учитывая, что распределение d(T) является биномиальным, получаем доверительные интервалы для параметра
с коэффициентом доверия не меньшим
= 1 — (
+
). Если к моменту Т окончания испытаний общее число отказов d(T) = d < r, то верхняя граница
доверительного интервала находится из уравнения
(36)
а нижняя — из уравнения
(37)
Если же момент появления r-го отказа tr<T, то верхняя граница находится из уравнения
(38)
а нижняя — из уравнения (39)
где S(tr) — суммарная наработка элементов к моменту tr.
Заметим, что , для случая tr>T
Для случая необходимо иметь таблицы решений уравнений (38), (39).
Если для выбранного значения r плана [N, Б, (r, T)] отношение , то планы [N, Б, (r, T)] и [N, B, (r, T)] практически эквивалентны; соответственно эквивалентны планы [N, B, r] и [N, Б, r], так как число заменяемых элементов составляет незначительную часть от их общего числа.
Поэтому в первом приближении для построения доверительных интервалов можно считать, что испытания проводились не по плану [N, Б, (r, T)], а по плану [N, B, (r, T)].
По той же причине оказываются практически эквивалентными доверительные интервалы, построенные исходя из плана [N, Б, r] и [N, B, r], если только наблюдаемое число d(T) отказавших элементов значительно меньше общего числа N испытываемых одновременно элементов, .
В начало
Содержание портала
0< <0,16∙(1+1,80); 0< <0,448.
Ответ: 0<<0,448.
Пример 3.
По данным 9 независимых равноточных измерений некоторой физической величины найдены среднее арифметическое результатов измерений =42,319 и «исправленное» среднее квадратическое отклонение s=5,0. Требуется оценить истинное значение случайной величины с надежностью
=0,95.
Решение.
Истинное значение случайной величины равно ее математическому ожиданию и задача сводится к нахождению доверительного интервала для оценки математического ожидания при неизвестном .

По заданным =0,95 и n=9 по таблице приложения 3 находим
=
.
Найдем доверительные границы:


Ответ: С надежностью =0,95 истинное значение измеряемой физической величины заключено в доверительном интервале 38,469<a<46,169.
Пример 4.
Построить доверительный интервал для оценки неизвестного математического ожидания нормального распределения при n=9, s=3, =6.
Решение.
Решим задачу двумя способами.
1) Примем в качестве среднего квадратического отклонения «исправленное» среднее квадратическое отклонение, т. е.
=s=3,
и найдем искомый доверительный интервал по формуле

По приложению 2 найдем из соотношения




тогда доверительный интервал для оценки математического ожидания равен
4,04<a<7,96.
2) Будем считать, что неизвестно и найдем искомый доверительный интервал по формуле

По таблице приложения 3 найдем
;




Таким образом, доверительный интервал равен
3,69<a<8,31
В первом случае длина интервала равна 7,96 – 4,04=3,92, во втором случае – 8,31 – 3,69=4,62.
Мы видим, что во втором случае с помощью закона Стьюдента получен более широкий доверительный интервал для оценки математического ожидания по сравнению с результатом, полученным для нормального закона распределения. При использовании t – распределения учитывается, что никакой дополнительной информации о дисперсии генеральной совокупности кроме той, которую дает выборка, нет. Поэтому использование при оценке математического ожидания нормального закона распределения при малом объеме выборки n и неизвестной дисперсии
привело бы к неоправданному сужению доверительного интервала.
Итак, для оценки математического ожидания нормального распределения по малым выборкам и неизвестном следует пользоваться t – распределением Стьюдента.
Пример 5.
Производят независимые испытания с одинаковой, но неизвестной вероятностью p появления события А в каждом испытании. Найти доверительный интервал для оценки вероятности p биномиального распределения с надежностью 0,95, если в 80 испытаниях событие А появилось 16 раз.
Решение.
По условию n=80; m=16; .
Найдем относительную частоту появления события А:

Найдем аргумент t функции Лапласа из соотношения

Найдем концы интервала p1 и p2:
Ответ: искомый доверительный интервал 0,128<p<0,299.
Пример 6.
Найти доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания а нормально распределенного признака Х генеральной совокупности, если генеральное среднее квадратическое отклонение , выборочная средняя
и объем выборки n=25.
Решение.
Требуется найти доверительный интервал

Все величины, кроме t, известны. Найдем t из соотношения Ф(t)=0,95/2=0,475. По таблице приложения 2 находим t=1,96. Подставив t=1,96, =14,
=5, n=25 в формулу, окончательно получим искомый доверительный интервал 12,04<a<15,96.
Контрольная работа
Задание № 1.
Найти внутригрупповую, межгрупповую и общую дисперсию совокупности, состоящей из трех групп.
I II III
|
1. |
|
|
|
||||||||||||||||||||||
|
2. |
|
|
|
||||||||||||||||||||||
|
3. |
|
|
|
||||||||||||||||||||||
|
4. |
|
|
|
||||||||||||||||||||||
|
5. |
|
|
|
||||||||||||||||||||||
|
6. |
|
|
|
||||||||||||||||||||||
|
7. |
|
|
|
||||||||||||||||||||||
|
8. |
|
|
|
||||||||||||||||||||||
|
9. |
|
|
|
||||||||||||||||||||||
|
10. |
|
|
|
Задание № 2
1. Найти доверительный интервал для оценки параметра нормального распределения с надежностью
по выборке:
,
если .
2. Событие А в серии из испытаний Бернулли произошло
раз. Найти интервальную оценку для вероятности Р событий А с надежностью

3. Найти минимальный объем выборки из нормальной генеральной совокупности, при котором с надежностью не меньшей , погрешность средней, найденная по этой выборке, будет меньше 0,3, если
.
4. Для оценки параметров нормально распределенной случайной величины была сделана выборка объема 30 и вычислено
. Найти доверительный интервал, покрывающий
с надежностью 0,90.
5. Производятся независимые испытания с одинаковой, но с неизвестной вероятностью Р появления события А в каждом испытании. Найти доверительный интервал для оценки Р с надежностью 0,95, если в 400 испытаниях событие А появилось 80 раз.
6. Количественный признак Х генеральной совокупности распределен нормально, по выборке объема 16 найдено . Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение с надежностью 0,999.
7. Глубина моря измеряется прибором, систематическая ошибка которого равна нулю, а случайные ошибки распределены нормально с см. Сколько надо сделать независимых измерений, чтобы определить глубину моря с ошибкой не более 5м при надежности 0,9?
8. Произведено 5 независимых наблюдений С. В. Х (нормальное распределение,неизвестно): x1=-25, x2=34, x3=-20, x4=10, x5=21. При уровне значимости 0,95 найти доверительный интервал для параметра
.
9. На контрольных испытаниях 16 осветительных ламп были определены: 
ч. Считая, что срок службы лампы является нормально распределенной С. В. Найти с надежностью 0,9 доверительный интервал для параметра
.
10. С. В. распределена по нормальному закону с параметром . По выборке объема
найти интервальную оценку параметра
.
Помогаю со студенческими работами здесь
Время безотказной работы станка имеет экспоненциальное распределение
Приветствую.
Собственно вот:
1) Время X безотказной работы станка имеет экспоненциальное…
Можно ли считать, что время безотказной работы этого прибора имеет нормальное распределение?
здрасвуйте, как решит это задача??
следующая информация представляют собой время безотказной…
Как найти среднее значение времени, не учитывая время, которое больше 2 часов?
Существует ряд времен
09:03:04
02:03:04
00:03:04
05:03:04
01:03:04
04:03:04
03:03:04…
За какое минимальное количество часов работы портные смогут изготовить одежду для 100 человек?
Подскажите как решить следующую задачу.
Старый портной шьет одну рубашку за 3 часа, а штаны 2…

Даны показания электронных часов и промежуток времени в виде часы минуты секунды. Определите…

Даны показания электронных часов в течение суток, которые определяют начало и конец промежутка…
Искать еще темы с ответами
Или воспользуйтесь поиском по форуму:

















