Торговая компания планирует к строительству три магазина - Контакты компаний и предприятий на Adresa.top

Задачи для самостоятельного решения

Задача
1.
Определить лучший инвестиционный
проект, рассчитав необходимые показатели
простым (статистическим) методом, сделать
вывод. Исходные данные приведены в
таблице.

Показатель	Значение показателя для проектов
1-го	2-го
Инвестиции, млн. руб.	620	740
Планируемая чистая прибыль по годам реализации проекта: млн. руб.:
1-й год	120	150
2-й год	150	170
3-й год	160	170
4-й год	170	170
5-й год	180	170
Жизненный цикл проекта, лет	7	7
Ставка банка по долгосрочным депозитам, %	10
Рентабельность совокупного капитала, %	25

Задача
2. Предприятие
инвестировало в инвестиционный проект
36000 тыс. рублей. Ожидаемая среднегодовая
величина прибыли от реализации
инвестиционного проекта составляет
10400 тыс. рублей. Рассчитать величину
нормы прибыли на капитал и срок окупаемости
инвестиционных затрат.

Задача
3.
Торговая компания планирует к строительству
три магазина розничной торговли. Первый
магазин площадью 1 500 кв. м, второй – 1
350, третий – 1 400 кв. м. Норматив удельных
капитальных вложений на 1 кв. м составляет
8 500 руб. для 1-го магазина, 8 100 руб. – для
2-го и 8 350 руб. – для 3-го магазина.
Планируемый объем прибыли от торговой
деятельности магазинов: 2,35 млн. руб. для
1-го магазина; 2,12 млн руб. – для 2-го и
2,48 млн руб. – для 3-го магазина. Рассчитайте
сумму капитальных вложений и сроки
окупаемости магазинов.

Задача
4. Предприниматель
принял решение об инвестировании
денежных средств в новый инвестиционный
проект. Первоначальные вложения составят
380 тыс. руб. Предполагаемые доходы от
реализации проекта составят: в 1-й год
– 105 тыс. руб., во 2-й год – 200 тыс. руб., в
3-й год – 190 тыс. руб., в 4-й год – 330 тыс.
руб., в 5-й год – 400 тыс. руб. Определить
срок окупаемости проекта.

Задача
5.
Рассчитайте срок окупаемости для
проекта, если капитальные затраты
составляют 11 000 тыс. рублей, остаточная
стоимость – 1 000 тыс. рублей, срок
проекта 5 лет, рабочий капитал – 4 000
тыс. рублей. Чистый денежный поток по
годам: 1 год – 4000, 2 год – 4000, 3 год – 4000,
4 год – 3000, 5 год – 2000 тыс. рублей.

Тема 5. Динамические методы оценки эффективности инвестиций

Цель:
изучение динамических методов оценки
инвестиционного проекта (основанных
на технике дисконтирования), выбор
наиболее эффективных вариантов
инвестиций.

Результат:
используя динамические методы, специалист
должен уметь оценивать экономическую
эффективность инвестиций, на основании
полученных данных давать оценку
эффективности инвестиционных вложений,
а также уметь выбирать из нескольких
инвестиционных проектов наиболее
эффективный проект.

Теоретические
сведения.
Сущность оценки инвестиционного проекта
заключается в адекватном определении
сегодняшних затрат и будущих поступлений.
Главный
недостаток простых (статистических)
методов оценки эффективности инвестиций
заключается в игнорировании факта
неравноценности одинаковых сумм
поступлений или платежей, относящихся
к разным периодам времени. Понимание и
учет этого фактора имеет большое значение
для корректной оценки проектов, связанных
с долгосрочным вложением капитала.

Поэтому
необходимо учитывать, что решение об
инвестировании применяется в настоящий
момент, а значит, показатели проекта
следует рассчитывать с учетом снижения
ценности денег в будущем.

Для
полноценной и более реалистичной оценки
финансовой эффективности проекта помимо
рассмотренных с вами ранее статистических
методов оценки инвестиций целесообразно
применять «динамические» методы,
основанные преимущественно на
дисконтировании образующихся в ходе
реализации проекта денежных потоков.
Применение дисконтирования позволяет
отразить основополагающий принцип
«завтрашние деньги дешевле сегодняшних»
и учесть тем самым возможность
альтернативных вложений по ставке
дисконта.

К
показателям оценки эффективности
инвестиций, основанным на применении
дисконтирования относятся:

чистая
приведенная стоимость (Net
Present Value, NPV);
индекс
доходности
(Profitability Index, PI);
внутренняя
норма
прибыли
(Internal
Rate of Return, IRR);
дисконтированный
срок окупаемости инвестиций (Discounted
Payback
Period,
DPP).

Суть
всех методов оценки базируется на
следующей простой схеме: Исходные
инвестиции при реализации какого-либо
проекта генерируют денежный поток CF₁,
CF₂,
… , CF_n.
Инвестиции
признаются эффективными, если этот
поток достаточен для:

возврата
исходной суммы капитальных вложений
и
обеспечения
требуемой отдачи на вложенный капитал.

Для
того чтобы оценить инвестиционный
проект, необходимо знать ставку
дисконтирования. Она представляет собой
ставку, по которой будущие денежные
поступления приводятся к текущей
стоимости. В качестве ставки дисконтирования
обычно выступает цена капитала
предприятия.

Чистая
приведенная стоимость
позволяет принять управленческое
решение о целесообразности реализации
проекта исходя из сравнения суммы
будущих дисконтированных доходов с
издержками, необходимыми для реализации
проекта (капитальными вложениями):

(21)

где
CF
— денежный
поток, соответствующего t
периода;

IC
– инвестируемый капитал;

r
— стоимость
капитала, привлеченного для инвестиционного
проекта.

В
соответствии с
сущностью
метода современное значение всех входных
денежных потоков сравнивается с
современным значением выходных потоков,
обусловленных капитальными вложениями
для реализации проекта. Разница между
первым и вторым есть чистое современное
значение, величина которого определяет
правило принятия решения:

для
отдельного проекта: если
NPV
больше или равно нулю, то проект
принимается;
для
нескольких альтернативных проектов:
принимается
тот проект, который имеет большее
значение NPV,
если только оно положительное.

Индекс
доходности
показывает отношение отдачи капитала
к размеру вложенного капитала, показатель
PI
показывает относительную прибыльность
проекта или дисконтируемую стоимость
денежных поступлений от проекта в
расчете на единицу вложений:

(22)

Рассматривая
показатель индекс
доходности,
необходимо принять во внимание то, что
данный показатель является относительным,
описывающим не абсолютный размер чистого
денежного потока, а его уровень по
отношению к инвестиционным затратам.
Это преимущество индекса прибыльности
инвестиций позволяет использовать его
в процессе сравнительной оценки
эффективности инвестиционных проектов,
различающихся по своим размерам (объему
инвестиционных затрат).

Критерий
принятия решения такой же, как при
принятии решения по показателю NPV,
т.е. РI
> 0. При этом возможны три варианта:

РI
> 1 – инвестиции рентабельны и приемлемы
в соответствии с выбранной ставкой
дисконтирования;
РI
< 1 – инвестиции не способны генерировать
требуемую ставку отдачи и неприемлемы;
РI
= 1 – рассматриваемое направление
инвестиций в точности удовлетворяет
выбранной ставке отдачи, которая равна
IRR.

Проекты
с высокими значениями PI
более устойчивы. Однако не следует
забывать, что очень большие значения
индекса доходности не всегда соответствуют
высокому значению чистой текущей
стоимости проекта и наоборот. Дело в
том, что проекты, имеющие высокую чистую
текущую стоимость не обязательно
эффективны, а значит, имеют весьма
небольшой индекс прибыльности.

Внутренняя
норма прибыли
представляет собой ту расчетную ставку
процента (ставку дисконтирования), при
которой сумма дисконтированных доходов
за весь период реализации инвестиционного
проекта становится равной сумме
первоначальных затрат (инвестициям):

,
.	(23)

IRR
показывает максимально допустимый
относительный уровень расходов, которые
могут быть ассоциированы с данным
проектом. Экономический смысл этого
показателя заключается в следующем:
предприятие может принимать любые
решения инвестиционного характера,
уровень рентабельности которых не ниже
текущего значения «цены» авансированного
капитала CC
(или цены источника средств для данного
проекта, если он имеет целевой источник).
Именно с ним сравнивается показатель
IRR,
рассчитанный для конкретного проекта,
при этом связь между ними такова:

IRR
> CC,
то проект следует принять;
IRR
< CC,
то проект следует отвергнуть;
IRR
= CC,
то проект ни прибыльный, ни убыточный.

Учитывая
характер формулы IRR,
следует отметить, что в явном виде
выразить IRR
можно только для уравнений второго и
третьего порядка. Для других случаев
можно воспользоваться формулой
Ньютона-Рафсона:

(24)

где
r₁
– коэффициент дисконтирования, при
котором NPV
проекта положительно;

NPV(r₁)
– положительное значение NPV;

r₂
– коэффициент дисконтирования, при
котором NPV
проекта отрицательна;

NPV(r₂)
– отрицательное значение NPV;

IRR
– внутренняя
норма доходности проекта.

Дисконтированный
срок окупаемости
разумно понимать как тот срок, в расчете
на который вложение средств в
рассматриваемый проект даст ту же сумму
денежных потоков, приведенных по фактору
времени (дисконтированных) к настоящему
моменту, которую за этот же срок можно
было бы получить с альтернативного
доступного для покупки инвестиционного
актива:

(25)

где
n
– число периодов;

CF_t–
приток денежных средств в период t;

r
–ставка дисконтирования;

IС
– величина исходных инвестиций.

При
использовании данного показателя в
оценке инвестиционных проектов решения
могут приниматься исходя из следующих
условий:

проект
принимается, если окупаемость имеет
место;
проект
принимается только в том случае, если
срок окупаемости не превышает
установленного для конкретной компании
предельного срока.

Срок
окупаемости увеличивается по сравнению
с расчетом его без дисконтирования (в
случае применения статистических
методов оценки).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Задачи по «Менеджменту»

Автор: • Декабрь 11, 2019 • Задача • 3,802 Слов (16 Страниц) • 340 Просмотры

Страница 1 из 16

Задача 1

В трех районах города предприниматель планирует строительство пользующихся спросом одинаковых по площади мини-магазинов «Продукты». Известны места, в которых их можно построить. Подсчитаны затраты на их строительство и эксплуатацию.

Необходимо так разместить магазины, чтобы затраты на их строительство и эксплуатацию были минимальны.

x	1	2	3	4	5
g1(x),	26	44	67	89	91
g2(x),	25	46	65	91	98
g3(x),	24	47	64	93	102

Решение:

Решение задачи проводим с использованием рекуррентных соотношений:

для первого района: φ1(x)=g1(x)

для остальных районов: φ k(x)= min{φ k(xk) + φ k-1(x- xk )}, k = [pic 1]

Задачу будем решать в три этапа.

1-й этап.

φ1(1)=g1(1)=26,

φ1(2)=g1(2)=44,

φ1(3)=g1(3)=67,

φ1(4)=g1(4)=89

φ1(5)=g1(5)=91

Если все магазины построить только в первом районе, то минимально возможные затраты при х = 5 составляют 91 ден.ед.

2-й этап. Определим оптимальную стратегию при размещении пяти магазинов только в первых двух районах по формуле:

φ 2(x)= min{φ 2(x2) + φ 2-1(x- x2 )}

Найдем φ2(l):

g2(1) + φ1(0) = 25 + 0 = 25,

g2(0) + φ1(l)= 0 + 26 = 26,

φ2(l) = min (25, 26) = 25.

Вычислим φ2(2):

g2(2) + φ1(0) = 46 + 0 = 46,

g2(l) + φ1(l) = 25 + 44 = 69,

g2(0) + φ1 (2) = 0 + 44 = 44,

φ2(2) = min (46, 69, 44) = 44.

Найдем φ2(3):

g2(3) + φ1 (0) = 65 + 0 = 65,

g2(2) + φ1(l) = 46 + 26 = 72,

g2(1) + φ1(2) = 25 + 44 = 69,

g2(0) + φ1(3) = 0 + 67= 67,

φ2(3) = min (65, 72, 69, 67) = 65.

Определим φ2(4):

g2(4) + φ1(0) = 91 + 0 = 91,

g2(3) + φ1(l) = 65 + 26 = 91,

g2(2) + φ1(2) = 46 + 44 = 90,

g2(l) + φ1(3) = 25 + 67 = 92,

g2(0) +φ1(4) = 0 + 89 = 89,

φ2(4) = min (91, 91, 90, 92, 89) = 89.

Определим φ2(5):

g2(5) + φ1(0) = 98 + 0 = 98,

g2(4) + φ1(l) = 91 + 26 = 117,

g2(3) + φ1(2) = 65 + 44 = 109,

g2(2) + φ1(3) = 46 + 67 = 113,

g2(l) + φ1(4) = 25 + 89 = 114,

g2(0) +φ1(5) = 0 + 91 = 91,

φ2(5) = min (98; 117; 109; 113; 114; 91) = 91.

3-й этап. Определим оптимальную стратегию при размещении пяти магазинов в трех районах по формуле:

φ3(x) = min{g3(x3) + φ2(x – х3)}.

Найдем φ3(5):

g3(5) + φ2(0) = 102 +0 = 102,

g3(4) + φ2(1) = 93 + 25 = 118,

g3(3) +φ2(2) = 64 + 44 = 108,

g3(2) + φ2(3) = 47 + 65 = 112,

…

Доступно только на Essays.club

Источник

Фирма имеет три магазина розничной торговли, расположенные в разных районах города (А, В, С).

Фирма имеет три магазина розничной торговли, расположенные в разных районах города (А, В, С). Поставки продукции в эти магазины осуществляются с четырёх складов (1, 2, 3, 4).
Магазины
А В С
№ склада
40 20 40
1 30 2 6 4
2 25 4 3 5
3 15 3 1 5
4 30 5 2 5
Найти оптимальное распределение поставок, при котором суммарные затраты на перевозку были бы минимальными.

Математическая модель транспортной задачи:F = ∑∑cijxij, (1)при условиях:∑xij = ai, i = 1,2,…, m, (2)∑xij = bj, j = 1,2,…, n, (3)xij ≥ 0
Запишем экономико-математическую модель для нашей задачи.
Переменные:x11 – количество груза из 1-го склада в 1-й магазин.x12 – количество груза из 1-го склада в 2-й магазин.x13 – количество груза из 1-го склада в 3-й магазин.x21 – количество груза из 2-го склада в 1-й магазин.x22 – количество груза из 2-го склада в 2-й магазин.x23 – количество груза из 2-го склада в 3-й магазин.x31 – количество груза из 3-го склада в 1-й магазин.x32 – количество груза из 3-го склада в 2-й магазин.x33 – количество груза из 3-го склада в 3-й магазин.x41 – количество груза из 4-го склада в 1-й магазин.x42 – количество груза из 4-го склада в 2-й магазин.x43 – количество груза из 4-го склада в 3-й магазин.Ограничения по запасам:x11 + x12 + x13 = 30 (для 1 склада)x21 + x22 + x23 = 25 (для 2 склада)x31 + x32 + x33 = 15 (для 3 склада)x41 + x42 + x43 = 30 (для 4 склада)Ограничения по потребностям:x11 + x21 + x31 + x41 = 40 (для 1-го магазина)x12 + x22 + x32 + x42 = 20 (для 2-го магазина)x13 + x23 + x33 + x43 = 40 (для 3-го магазина)Целевая функция:2×11 + 6×12 + 4×13 + 4×21 + 3×22 + 5×23 + 3×31 + 1×32 + 5×33 + 5×41 + 2×42 + 5×43 → min
Проверим необходимое и достаточное условие разрешимости задачи.∑a = 30 + 25 + 15 + 30 = 100∑b = 40 + 20 + 40 = 100
Условие баланса соблюдается

. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой.
Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.
Отыскиваемый элемент равен c32=1. Для этого элемента запасы равны 15, потребности 20. Т.к. минимальным является 15, то вычитаем его.x32 = min(15,20) = 15.
2 6 4 30
4 3 5 25
x 1 x 15 — 15 = 0
5 2 5 30
40 20 — 15 = 5 40
Отыскиваемый элемент равен c11=2. Для этого элемента запасы равны 30, потребности 40. Т.к. минимальным является 30, то вычитаем его.x11 = min(30,40) = 30.
2 x x 30 — 30 = 0
4 3 5 25
x 1 x 0
5 2 5 30
40 — 30 = 10 5 40
Отыскиваемый элемент равен c42=2. Для этого элемента запасы равны 30, потребности 5

Фирма «Инвест-строй» получила пакет разрешительной документации на строительство в предстоящие полтора года трех жилых
Фирма использует 400 тыс. единиц материала в год. Стоимость каждого заказа равна 200 тыс.
Фирма использует 400 тыс. единиц материала в год. Стоимость каждого заказа равна 200 тыс.. 2
Фирма использует в производстве товара А два независимых ресурса: L и К (труд и
Фирма «Картон» планирует инвестиции в новое оборудование 900 тыс. руб. Ожидаемый ежегодный чистый денежный
Фирма «Кидалия» функционирует на рынке совершенной конкуренции с общими затратами, формализуемыми следующей функцией:
Фирма стремилась
Фирма «Кристалл» осуществляет в налоговом периоде импорт в Россию партии автомобилей, в том числе
Фирма имеет возможность приобрести не более 15 трехтонных автомашин и не более 22 пятитонных.
Фирма имеет два магазина и торгует тремя товарами в течение года. Проводя расчеты в
Фирма имеет производственную функцию вида: Q = 14*(L^0,5)*(K^0,5).
Цена единицы фактора труд PL=10*14=140, единицы фактора
Фирма имеет ряд финансовых обязательств перед одним кредитором – S_1 млн. рублей,〖 S〗_2 млн.
Фирма имеет ряд финансовых обязательств перед одним кредитором – S1 млн. рублей, S2 млн.
Фирма имеет ряд финансовых обязательств перед одним кредитором – S1 млн. рублей, S2 млн.. 2
Фирма имеет следующий баланс:
АКТИВ
ПАССИВ
Денежные средства 300 Кредиторская задолженность 300
Дебиторская задолженность 500 Задолженность

Источник

Ростов-на-Дону ,

21 мар, 16:41

Компания «Флэш» планирует построить три автоматические автомобильные мойки в Ростове-на-Дону к середине 2024 года. Новые объекты появятся на улицах Чемордачка, Левобережная, Доватора. Сейчас компания готовит материалы для прохождения публичных слушаний на установление условно разрешенного вида участков, сообщил начальник отдела развития сети АЗС Евгений Кейдунов в ходе заседания Совета по инвестициям.

«Проект состоит из трех элементов — строительство АЗС, строительство автоматических автомобильных моек и «умный магазин». Часть объектов уже реализовали на территории Ростовской области и Ростова-на-Дону. На ул. Орская автоматическую мойку ввели в эксплуатацию в 2022 году. В настоящее время ведем строительство на ул. Курская», — рассказал Кейдунов.

По его словам, на разработку проектной документации потребуется порядка 2-4 месяцев, а на строительно-монтажные работы — 2-3 месяца. Кроме того, компания планирует построить в Ростове-на-Дону «умный» магазин, в котором приобретение товаров будет реализовываться при помощи биометрических данных покупателей.

«Сейчас объект «умный» магазин — это автоматическая заправочная станция. Находится на ул. Виталия Ходоша, участок в нашей аренде. Мы видим реализацию этого проекта через проектирование, прохождение экспертизы по реконструкции этого объекта в многокомплексный многофункциональный объект», — добавил Кейдунов.

Согласно реестру инвестиционных проектов, размещенном на сайте донского правительства, ООО «Флэш» с 2022 года начало реализовывать проект, предусматривающий строительство строительство 5 автоматических АЗС в Ростове, Новочеркасске и селе Песчанокопское, еще 6 автоматических автомобильных моек в Ростове, Шахтах, Аксайском районе, а также двух модульных АЗС в Тарасовском районе и «умного» магазина в Ростове. Проект планируют завершить в 2026 году. Сумма инвестиций оценивается 1,1 млрд рублей.

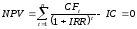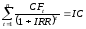Источник